2.4 Dynamika sústavy hmotných bodov a telesa
2.4.1 Dynamika sústavy hmotných bodov
Sily, ktoré pôsobia na
sústavu hmotných bodov (častíc) možno rozdeliť na sily vonkajšie a vnútorné. Pod vonkajšími silami budeme rozumieť sily, ktoré majú príčinu v pôsobení
okolitých telies, ktoré do sústavy hmotných bodov nepatria, ale pôsobia na jednotlivé častice sústavy ( i = 1, ..., n) . Výslednicu vonkajších
síl pôsobiacich na i-tu časticu
označme Fi .
Sily vnútorné majú podstatu vo
vzájomnom pôsobení jednotlivých častíc sústavy. Charakterizujú interakcie medzi
jednotlivými časticami vo vnútri sústavy. Označme symbolom Fij
tú vnútornú silu, ktorou pôsobí j-ta
častica na i-tu časticu
a symbolom Fvi výslednicu všetkých
vnútorných síl pôsobiacich na i-tu
časticu od okolitých častíc. Fvi bude určená vzťahom
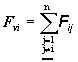 (2.4.1)
(2.4.1)
Celková
sila pôsobiaca na i-tu častica Fci
je súčtom celkovej vonkajšej sily a celkovej vnútornej sily pôsobiacej na i-tu časticu, t.j.
![]() (2.4.2)
(2.4.2)
Celá
sústava častíc je podrobená silám
![]() (2.4.3)
(2.4.3)
Keďže
podľa zákonu akcie a reakcie platí Fij
= - Fji , posledný člen
s dvojitou sumáciou sa rovná nule. Rovnicu (2.4.4) možno interpretovať
nasledovne: Zmenu pohybového stavu
sústavy hmotných bodov (častíc) spôsobuje sila F, ktorá sa rovná
vektorovému súčtu vonkajších síl pôsobiacich na sústavu.
![]() (2.4.4)
(2.4.4)
Ak
výslednica všetkých vonkajších síl
pôsobiacich na sústavu je nulová (F = 0), hovoríme, že sústava je izolovaná.
Hybnosť sústavy častíc a I. veta
impulzová
Definujme celkovú hybnosť sústavy
častíc ako vektorový súčet
hybností jednotlivých častíc
![]() (2.4.5)
(2.4.5)
kde mi je hmotnosť i-tej častice a vi
je rýchlosť i-tej
častice. Celkovú hybnosť sústavy hmotných bodov môžeme vyjadriť i cez
myslený hmotný bod, ktorý sa nachádza v hmotnom strede sústavy
a v ktorom je sústredená celková hmotnosť. Rýchlosť hmotného stredu získame deriváciou jeho polohového
vektora, (vzťah (2.2.1):
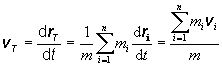 (2.4. 6)
(2.4. 6)
Pre
jeho hybnosť platí
![]() (2.4.7)
(2.4.7)
Celková hybnosť sústavy hmotných bodov sa rovná hybnosti mysleného bodu,
ktorý sa nachádza v hmotnom strede sústavy. Tento bod sa pohybuje rovnakou
rýchlosťou s akou sa pohybuje
hmotný stred a má hmotnosť celkovej hmotnosti sústavy. Zrýchlenie
hmotného stredu dostaneme deriváciou vzťahu (2.4.7):
![]() (2.4.8)
(2.4.8)
![]() (2.4.9)
(2.4.9)
Ľavú
stranu rovnice (2.49) možno vyjadriť pomocou síl pôsobiacich v sústave:
![]() (2.4.10)
(2.4.10)
V poslednom
súčte každý člen znamená celkovú silu pôsobiacu na i-ty hmotný bod. Uvažujme teraz sily pôsobiace na každý hmotný bod
sústavy. Nakoľko pre i-tu časticu platí Newtonov zákon, možno
pohybovú rovnicu pre sústavu hmotných častíc, na základe vzťahu
(2.4.4) vyjadriť
![]() (2.4.11)
(2.4.11)
resp.
pomocou celkovej hybnosti ako
![]() (2.4.12)
(2.4.12)
Rovnica (2.4.12) vyjadruje pohybový zákon pre
sústavu hmotných bodov, ktorý
možno interpretovať: Zmena celkovej
hybnosti sústavy za jednotku času sa rovná výslednici vonkajších síl
pôsobiacich na sústavu. Vnútorné sily
celkovú hybnosť sústavy neovplyvňujú. Rovnicu (2.4.12) možno vyjadriť i pomocou
fyzikálnej veličiny impulz sily I :
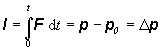 (2.4.13)
(2.4.13)
Vzťah (2.4.13)
nazývame 1. veta impulzová a možno ju interpretovať: Impulz
vonkajších síl pôsobiacich na sústavu hmotných bodov (častíc) sa rovná
zväčšeniu celkovej hybnosti sústavy hmotných bodov .
Spojením rovnice 2.4.4 a 2.4.10 dostaneme pre zrýchlenie hmotného
stredu rovnicu, ktorú nazývame veta o pohybe hmotného stredu:
![]() (2.4.14)
(2.4.14)
Hmotný stred sa pohybuje ako hmotný bod, do ktorého je sústredená celková
hmotnosť sústavy a v ktorom pôsobí výslednica vonkajších síl.
Vnútorné sily nemajú vplyv na pohyb hmotného stredu.
Moment hybnosti sústavy častíc a II. veta impulzová
Moment hybnosti sústavy častíc definujme obdobným spôsobom ako bol definovaný moment hybnosti i -tej častice vzhľadom na vzťažný bod O:
![]() (2.4.15)
(2.4.15)
kde ri
je polohový vektor i -tej častice vzhľadom
na zvolený vzťažný bod, pi je hybnosť i -tej častice. Pre i -tu časticu platí
rovnica
![]() (2.4.16)
(2.4.16)
pretože
pre moment sily každej častice platí
![]()
Rovnicu
(2.4.16) možno interpretovať : Moment na i -tu časticu pôsobiacej sily sa
rovná zmene jeho momentu hybnosti za jednotku času. Obidva momenty
vzťahujeme na ľubovolný, avšak pre obidva momenty ten istý vzťažný bod v inerciálnej sústave. Celkový moment
sústavy častíc definujme vektorovým súčtom jednotlivých momentov
![]() (2.4.17)
(2.4.17)
Moment
sily Mi pôsobiacej na i -tu časticu možno vyjadriť pomocou
celkovej sily pôsobiacej na i -tu
časticu rovnicou, ktorú sme označili symbolom Fci
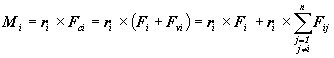
Po dosadení
do vzťahu (2.4.17) dostaneme pre celkový moment výslednej sily pôsobiacej na
sústavu častíc vzťah
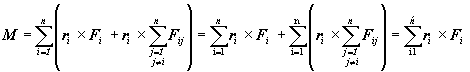 (2.4.18)
(2.4.18)
pretože
druhý člen v (2.4.18) je nulový, nakoľko v dvojnásobnej sume sa
nachádzajú vždy dvojice, pre ktoré
platí
![]()
(Poznámka:
Vektorový súčin je nulový, pretože vektor
![]() je rovnobežný
s vektorom Fij.)
je rovnobežný
s vektorom Fij.)
Celkový moment hybnosti sústavy častíc L
je definovaný ako vektorový
súčet momentov hybnosti jednotlivých
častíc, t.j.
![]() (2.4.19)
(2.4.19)
Pre
celkový moment výslednice vonkajších síl
pôsobiacich na sústavu častíc vzhľadom na zvolený vzťažný bod, po využití rovnice (2.4.19), dostávame
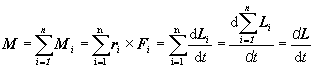 (2.4.20)
(2.4.20)
Rovnica
(2.4.20) predstavuje druhú pohybovú rovnicu pre sústavu hmotných bodov
(častíc). Jej úpravou dostaneme II. vetu impulzovú
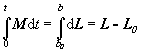 (2.4.21)
(2.4.21)
Význam
II. vety impulzovej je : Impulz momentov
vonkajších vzhľadom na zvolený ľubovolný bod sa rovná prírastku jeho celkového
momentu hybnosti.
Zákony zachovania
Ak aplikujeme na I. a II. vetu impulzovú podmienku platnú pre
uzavretú sústavu, t.j. výsledná
vonkajšia sila pôsobiaca na sústavu hmotných bodov je nulová a hmotnosť
sústavy sa nemení, získame zákon zachovania :
1/ Zákon zachovania hybnosti:
Celková hybnosť izolovanej sústavy
hmotných bodov ostáva konštantná, t.j. platí
p = p0 (2.4.22)
kde p0 je
hybnosť sústavy v časovom okamžiku na začiatku skúmania sústavy hmotných
bodov a p je hybnosť sústavy
hmotných bodov v okamžiku
skončenia skúmania sústavy.
Zákon zachovania hybnosti možno
zapísať i v tvare p = konst. Rovnica
(2.4.22) je vektorová rovnica, ktorá je ekvivalentná trom skalárnym
rovniciam. V istých prípadoch,
podľa silového pôsobenia na sústavu hmotných bodov, môžu nastať prípady, kedy
sa zachováva jedna, alebo dve zložky
celkovej hybnosti. V prípade, že len niektorá zo zložiek výslednice
vonkajších síl pôsobiacich na sústavu hmotných bodov je rovná nule, potom sa
odpovedajúca zložka celkovej hybnosti sústavy hmotných bodov zachováva. Ako
príklad môžeme uviesť skúmanie pohybu
letiaceho kameňa v gravitačnom poli Zeme. Ak zanedbávame odpor prostredia,
jedinou pôsobiacou silou na kameň je tiažová sila G = mg, ktorá smeruje zvisle
nadol (g = [0,-g,0]). Zvislá
zložka hybnosti letiaceho kameňa py sa bude meniť, kým zložky px a pz zostávajú konštantné.
Zmenu celkového mementu
hybnosti uzavretej sústavy možno dosiahnuť len pôsobením vonkajších síl.
Pôsobením vnútorných síl môžeme dosiahnuť len zmenu hybnosti jednotlivých
bodov (častíc) sústavy, avšak nie zmenu celkovej hybnosti sústavy.
________________________________
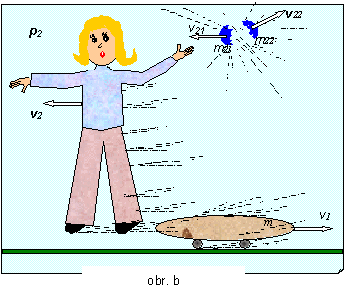
Príklad 2.4.1 Na skyborde o hmotnosti m, ktorý sa pohybuje
konštantnou rýchlosťou v0
stojí dievča o hmotnosti m1 a
v ruke drží sklenenú guľu s hmotnosťou m2.. . Sklenená guľa sa náhle roztrhne na dve
časti, pričom časť gule
s hmotnosťou m21
odletela rýchlosťou v21 opačným
smerom ako pohybujúci sa skybord, Druhá časť gule s hmotnosťou m22 sa pohybovala rýchlosťou v22
v smere zvierajúcim
s pohybujúcim sa vozíkom uhol a. Dievča v okamžiku roztrhnutia gule od ľaku zoskočí
zo skybordu v opačnom smere pôvodného
pohybu skybordu rýchlosťou v2. Určite rýchlosť v1 prázdneho skybordu, , ktorou
sa pohyboval v okamžiku roztrhnutia gule.

Riešenie: Sústava častíc, ktorú skúmame
sa skladá na začiatku skúmania zo
skybordu, na ktorom sa vezie dievča
s guľou. Označme hybnosť tejto sústavy p1. Po roztrhnutí
gule sústava sa skladá z pohybujúceho sa dievčaťa s hybnosťou p,
pohybujúceho sa vozíka
s hybnosťou p2 a pohybujúcich sa dvoch častí gule
s hybnosťami p21 a p22. Ak zanedbáme silu trenie
skybordu a odporu vzduchu, na každú časť sústavy pôsobí len tiažová sila. Keďže tiažová sila má zvislý
smer, neprispieva k zmene vodorovnej zložky celkovej hybnosti sústavy.
Vodorovná (x -ová) zložka hybnosti sústavy sa zachováva a platí pre ňu zákon zachovania
hybnosti, t.j. vodorovná zložka hybnosti sústavy pred roztrhnutím gule sa rovná
vodorovnej zložke hybnosti sústave v okamžiku roztrhnutia gule.
Matematické vyjadrenie zákona zachovania hybnosti v súradnicovej sústave s
kladnou osou x v smere pohybu skybordu pred roztrhnutím gule je dané rovnicou
p1x= px +p2x+
p21x + p22x (1)
Po dosadení x-vých zložiek jednotlivých rýchlostí pred roztrhnutím : v0 = [ v0,
0 ] a po
roztrhnutí:
v1 = [ v1,
0 ] , v21 = [- v21, 0 ], v22
= [ v22 cos
a , v22 sin
a ], v2
= [-v2, 0 ] do rovnice (1)
dostaneme
![]()
odkiaľ hľadanú rýchlosť prázdneho
skybordu v1 vyjadríme
![]()
2/
Zákon zachovania momentu hybnosti:
Celkový moment
hybnosti izolovanej sústavy hmotných bodov ostáva konštantný, t.j. platí
L = L0 (2.4.23)
Overenie platnosti zákona zachovania momentu
hybnosti možno uskutočniť ako pre dve telesá, tak i pre uzavretý systém.
Prvý príklad možno demonštrovať s chlapcom sediacim na stoličke s otáčajúcim sa sedadlom, ktorý drží činky v úplne roztiahnutých
rukách. Nech sediaceho chlapca niekto uvedie do pomalého otáčavého pohybu.
V prípade, že chlapec nehybne sedí na stoličke, otáčajúca sa stolička
v dôsledku trenia bude zmenšovať
svoju rýchlosť otáčania sa, až kým sa nezastaví. Stane sa nejaká zmena
v tomto pohybe, ak chlapec
rýchlo pritiahne činky k hrudi
a opätovne ich roztiahne?
Ak v otáčajúcom sa systéme chlapec rýchlo pritiahne ruky s činkami
na prsia, zistí, že jeho rýchlosť otáčania sa
zväčšuje. Ak ich roztiahne pohyb sa spomaľuje. Kým sa stolička trením
nezastaví, môže chlapec týmto spôsobom niekoľkokrát meniť svoju rýchlosť
otáčania.
Zväčšenie rýchlosti otáčania súvisí so zmenšením vzdialenosti
činiek od osi otáčania. Na rovnakom
princípe sú založené pohyby akrobatov alebo baletky, ktorá sa rýchlo
otáča. Obvykle dostáva baletka
začiatočný moment impulzu od svojho partnera. Vtedy je telo baletky naklonené,
začína sa pomalé otáčanie, potom nasleduje prekrásny a rýchly pohyb
–baletka sa narovnala. V tejto polohe sú všetky časti tela bližšie
k rotačnej osi a zákon
zachovania momentu hybnosti spôsobí prudké zvýšenie rýchlosti otáčania.
3/ Zákon zachovania celkovej energie
Uvažujme i-ty hmotný bod sústavy hmotných bodov. Zmena kinetickej energie DEki, , podľa vety o kinetickej energie (2.3.45), sa rovná práci všetkých síl pôsobiacich na vybraný hmotný bod. Teda práci síl vnútorných Aiint i práci síl vonkajších Aiext pôsobiacich na i-ty hmotný bod, čo možno zapísať
![]() (2.4.24)
(2.4.24)
Ak sčítame tieto rovnice
pre všetky hmotné body dostaneme
![]()
![]() (2.4.25)
(2.4.25)
Vnútorné sily sú konzervatívne,
preto ich prácu môžeme vyjadriť na základe vzťahu (2.3.51) ako pokles potenciálnej energie -DEp..
![]()
![]() (2.4.26)
(2.4.26)
Rovnica (2.4.26)
hovorí, že pre sústavu hmotných bodov
zmena celkovej mechanickej energie sústavy sa rovná práci vonkajších
síl. Ak máme systém izolovaný, výslednica vonkajších síl je nulová a teda
i práca tejto sily je nulová a platí
D(Ek + Ep )
= 0 (2.4.27)
resp.
Ek +Ep = konst
(2.4.28)
V izolovanej sústave hmotných
bodov celková mechanická energia sa zachováva.