2.3.9 Impulz sily, I. veta impulzová

 

Nech  hmotný bod  o  hmotnosti m má v časovom okamihu t₁  rýchlosť v_1, resp.  hybnosť p₁ = mv₁ a v časovom okamihu t₂ rýchlosť v_2, resp.  hybnosť p₂ = mv₂ . Ak počas časového intervalu Dt = t₂ –t₁   sa hmotný bod pohybuje pod účinkom sily F, Newtonovu pohybovú rovnicu možno prepísať do rovnice

 

 

Po integrovaní  dostávame

   

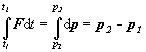                                                                                                     (2.3.59)

 

 

Integrál  sa nazýva impulz sily

 

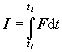                                                                                                                    (2.3.60)

 

Ak pôsobiaca sila je konštantná, impulz sily možno vyjadriť

 

 

                                                                                                                    (2.3.61)

 

V prípade ak sila nie je konštantná a nepoznáme jej časový priebeh,  ale  poznáme počiatočnú a konečnú hodnotu hybnosti hmotného bodu, môžeme určiť strednú hodnotu silu pôsobiacej na hmotný bod počas časového intervalu Dt vzťahom.

 

                                                                                                                   (2.3.62)

 

Rovnicu

 

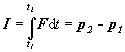                                                                                                          (2.3.63)

 

možno slovne vysloviť: Impulz sily pôsobiacej na voľný hmotný bod sa rovná zmene hybnosti hmotného bodu. Rovnicu (2.3.63) nazývame tiež  prvá veta impulzová pre hmotný bod.

 

Kontrolné otázky k časti 2.3.9

 

1.     Definujte veličinu impulz sily.

2.     Napíšte jednotku impulzu sily pomocou základných veličín SI.

3.     Aký účinok sily vyjadruje veličina impulz sily?

4.     Vyjadrite impulz sily, ak pôsobiaca sila je konštantná.

5.     Matematicky formulujte a vysvetlite prvú vetu impulzovú.