2.3 Dynamika hmotného bodu
2.3.1 Základné pojmy
· Dynamika
Zaviedli sme si pojem hmotný bod, pod ktorým rozumieme skúmaný objekt, ktorý má z hľadiska vzájomného pôsobenia s inými objektmi všetky vlastnosti skúmaného telesa, avšak neuvažujeme jeho geometrické rozmery.
Dynamika sa zaoberá príčinami pohybu. Dynamika skúma vzájomné pôsobenie medzi hmotnými
objektmi. (Pozn. Názov dynamika je odvodený z gréckeho slova dynamis
(sila).) Vzájomné pôsobenie telies, resp. fyzikálnych polí, má za následok buď zmenu ich pohybového
stavu, alebo deformáciu telies, alebo súčasne obidvoje. Pri deformácii máme na
mysli buď zmenu objemu, alebo zmenu tvaru
telesa. Dynamika je časť
mechaniky, ktorá skúma závislosť medzi pohybom telies a silami,
ktoré na ne pôsobia a vyvolávajú zmeny ich pohybového stavu. Ak vyšetrujeme
pohyb objektu, ktorého rýchlosť je značne menšia ako je rýchlosť svetla vo
vákuu t.j. v << c, hovoríme
o dynamike klasickej nerelativistickej mechaniky ( tzv. newtonovskej
mechaniky).
·
Izolovaná
vzťažná sústava
Prv než
začneme uvažovať pohyb, musíme si uvedomiť v akej vzťažnej sústave budeme vzájomné pôsobenie
charakterizovať. V kinematike nie
je principiálny rozdiel medzi rôznymi vzťažnými sústavami. Z hľadiska
kinematiky sú všetky rovnocenné. Inak je tomu
pri štúdiu zákonov pohybu z hľadiska dynamiky. Pri rôznych
vzťažných sústavách. možno, ako si neskôr ukážeme, dospieť k rôznym
výsledkom, niekedy podstatne zložitejším.
Preto je vhodné zadefinovať takú vzťažnú sústavu, v ktorej
zrýchlenie hmotného bodu bude spôsobené len vzájomným pôsobením tohto hmotného
bodu s inými telesami vo vnútri sústavy. Ak sústavu dostatočne vzdialime
od ostatných materiálnych objektov, t.j. od pôsobenia vonkajších síl, možno zadefinovať izolovanú vzťažnú sústavu.
Pod izolovanou sústavou rozumieme sústavu, na ktorú nepôsobia žiadne ďalšie objekty, t.j. nepôsobia žiadne vonkajšie sily. To isté možno vyjadriť, ak povieme, že výslednica všetkých vonkajších síl je rovná nule. resp. vektorový súčet všetkých pôsobiacich vonkajších síl je rovný nule
![]()
Poznámka: Túto skutočnosť umožňuje poznatok, že veľkosť sily pôsobiacej medzi dvomi telesami klesá s ich vzdialenosťou a nie pomalšie ako s kvadrátom ich vzdialenosti.
·
Inerciálna
vzťažná sústava
Inerciálna vzťažná sústava, resp. inerciálna sústava je postulovaná na základe prvého a druhého Newtonovho zákona ako vzťažná sústava, v ktorej platí Newtonov zákon zotrvačnosti a Newtonov zákon sily, o ktorých bližšie pojednáva časť 2.3.2.
Ak sústava S je inerciálna, potom každá sústava S´, ktorá sa vzhľadom na sústavu pohybuje s konštantnou rýchlosťou v0 , takým spôsobom, že jednotlivé osi sústavy S´ majú vzhľadom na osi sústavy S stále ten istý smer, je tiež inerciálnou súradnicovou sústavou.
Skôr ako Newton formuloval svoje pohybové zákony Galileo Galilei (1564-1642) došiel k záveru, že mechanický pohyb telies je rovnaký vo
všetkých vzťažných sústavách, ktoré sa pohybujú rovnomerne a priamočiaro a
riadi sa rovnakými zákonmi pohybu. Táto skutočnosť je známa ako samostatný
fyzikálny princíp nazvaný Galileov
princíp relativity. V rámci Newtonovskej mechaniky ho možno
formulovať: Všetky inerciálne vzťažné sústavy sú rovnocenné, pretože mechanický
pohyb telies vzhľadom na každú
z nich sa riadi tými istými zákonmi, ktorými sú Newtonove pohybové zákony. Z tohto dôvodu nemôžeme žiadnu
inerciálnu sústavu preferovať, všetky sú rovnocenné. Prakticky sa to prejaví
tým, že nie je možné žiadnymi mechanickými experimentami, uskutočnenými vo
vnútri určitej vzťažnej sústavy, rozhodnúť, či je uvažovaná sústava
v pokoji, alebo sa pohybuje rovnomerným priamočiarym pohybom. Inými
slovami možno povedať, že ak sa
v dvoch sústavách, pohybujúcich sa rovnomerným priamočiarym pohybom, vytvoria
rovnaké počiatočné podmienky určitého deja, potom tento dej bude prebiehať
celkom rovnako v obidvoch sústavách.
Príkladom inerciálnej sústavy je súradnicovú sústavu, ktorej začiatok je v strede slnečnej sústavy a ktorej súradnicové osi smerujú k trom vzdialeným hviezdam neležiacim v jednej rovine. (tzv. Koperníkova sústava, ktorú možno považovať za sústavu bez zrýchlenia). Ľubovolnú inú sústavu, pohybujúcu sa bez zrýchlenia vzhľadom na sústavu pevne spojenú so stálicami (Koperníkovu) nazývame inerciálnou.
Sústava, ktorá nie je inerciálna sa nazýva neinerciálna. Pod neinerciálnou sústavou rozumieme každú sústavu, ktorá koná zrýchlený priamočiary pohyb, alebo ktorá koná rotačný pohyb.
Vzťažná sústava pevne spojená so Zemou nie je inerciálna. Je to v dôsledku toho, že sa Zem pohybuje zrýchlene vzhľadom na Koperníkovu sústavu. Rotačný pohyb Zeme spôsobuje odchýlky, ktoré možno charakterizovať tzv. zotrvačnými silami, o ktorých sa zmienime neskôr. Ak však časový interval, v ktorom skúmame daný dej je taký, že pohyb Zeme v dôsledku jej rotácie možno zanedbať, môžeme pre väčšinu fyzikálno-technických problémov považovať sústavu pevne spojenú so Zemou za inerciálnu.
·
Hmotnosť
Najvýznamnejšou dynamickou charakteristikou telies je ich hmotnosť (značka m). Jej jednotkou v SI sústave je kilogram (kg). 1 kg sa rovná hmotnosti medzinárodného prototypu kilogramu. Táto definícia bola zavedená už v roku 1889 a potvrdená ako jednotka hmotnosti (nie váhy) v roku 1901. Medzinárodný prototyp kilogramu je vyrobený zo zliatiny platiny a irídia a je uložený za presne určených podmienok v Medzinárodnom úrade pre miery a váhy v Sevres pri Paríži.
Hmotnosť je kladná skalárna veličina, ktorá charakterizuje základnú vlastnosť všetkých hmotných objektov, ktorou je ich zotrvačnosť a ich vzájomné gravitačné pôsobenie.
Zo skúsenosti vieme, že ak dve guľôčky o rôznych hmotnostiach dáme do pohybu rovnako veľkými silami, za rovnaký časový interval, guľôčka s menšou hmotnosťou dosiahne väčšiu rýchlosť, ako guľôčka s väčšou hmotnosťou. Na dosiahnutie rovnakej rýchlosti guľôčky s väčšou hmotnosťou za ten istý časový interval, potrebujeme pôsobiť väčšou silou. Hmotnosť nám teda naznačuje akúsi mieru „odporu telesa“ proti zmene pohybového stavu. Vlastnosť telesa nemeniť svoj pohybový stav, teda rýchlosť, nazývame zotrvačnosťou. V tomto prípade hovoríme o zotrvačnej hmotnosti. S jej ďalším vysvetlením sa stretneme pri druhom Newtonovom zákone.
Podľa Newtonovho gravitačného zákona, o ktorom bližšie pojednáva časť 2.5.2, je veľkosť príťažlivých gravitačných síl, ktorými na seba pôsobia navzájom dva hmotné body, priamo úmerná hmotnosti každého z nich a nepriamoúmerná kvadrátu ich vzájomnej vzdialenosti. Táto hmotnosť sa nazýva gravitačná hmotnosť. Určujeme ju vážením.
Pri pozornom štúdiu si môžeme
položiť otázku: Je zotrvačná hmotnosť
rovnaká s gravitačnou hmotnosťou? Bolo uskutočnených množstvo
experimentov. Pri všetkých doteraz urobených meraniach bolo zistené, že
v medziach relatívnej presnosti,
minimálne 10-12, je gravitačná hmotnosť telesa vždy rovná jej
zotrvačnej hmotnosti. Preto obyčajne tieto hmotnosti nerozlišujeme. Hmotnosť
zotrvačná a hmotnosť gravitačná sú identické a označujú sa jedným spoločným
názvom hmotnosť.
Hmotnosť je
veličina aditívna a v newtonovskej fyzike je hmotnosť určitého telesa
konštantná, nezávislá od jeho pohybového stavu.
·
Hybnosť hmotného bodu
Hybnosť hmotného bodu resp. telesa je vektorová veličina definovaná ako skalárny násobok vektora rýchlosti hmotnosťou hmotného bodu (častice).
p = m v (2.3.1)
Jednotkou hybnosti je v SI sústave je kilogram meter za sekundu, kg.m.s-1.
Pozn.: Pri
riešení problémov si musíme uvedomiť, že
ak sa pri zmene smeru pohybu telesa veľkosť rýchlosti nezmení, zmena hybnosti ![]() p , určená vzťahom
p , určená vzťahom
Dp= m (v 2 - v 1) = m Dv (2.3.2)
bude nenulová, nakoľko Dv je nenulový vektor, pretože v dvoch rôznych časových okamihoch teleso má rýchlosti v1 a v2, pre ktoré platí v 2 ¹ v 1 .
·
Moment
hybnosti hmotného bodu
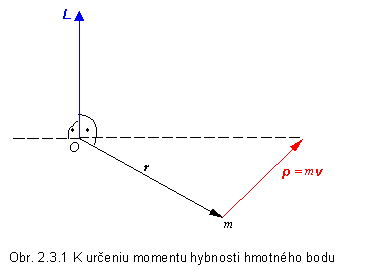
Vektorová veličina L, moment hybnosti bodu vzhľadom na zvolený bod O, je definovaná vektorovým súčinom polohového vektora r hmotného bodu so začiatkom v bode O a hybnosti p hmotného bodu (obr. 2.3.1)
L = r
´ p (2.3.3)
Moment hybnosti hmotného bodu je teda vektor, ktorý má veľkosť rovnú ploche rovnobežníka určeného vektormi r a p , resp. súčinu rmv sin a , kde a je uhol, ktorý zvierajú vektory r a p. Moment hybnosti L má smer kolmý na rovinu určenú vektormi r a p. Jednotkou momentu hybnosti v SI sústave je kilogram meter na druhú za sekundu, kg .m2.s-1.
· Sila
Pri experimentálnom skúmaní rôznych pohybov sa zistilo, že každé
zrýchlenie skúmaného objektu (hmotného bodu) je spôsobené nejakými inými
hmotnými objektmi, resp. telesami. Na
charakterizovanie miery tohoto vzájomného pôsobenia medzi materiálnymi objektmi
sa zaviedla veličina, ktorú nazývame sila (značka F). Sila F je vektorová fyzikálna
veličina, vyjadrujúca kvantitatívne pôsobenie materiálnych objektov resp.
fyzikálnych polí. Jej jednotkou v SI sústave je newton (značka
N ). 1 N je sila, ktorá udeľuje telesu (hmotnému bodu) s
hmotnosťou 1 kg zrýchlenie 1 m.s-2.
Platí teda 1 N =1 kg.m.s-2.
Práve na zobrazovanie súčasného pôsobenia viacerých síl na hmotný bod boli po prvý raz použité vo fyzike vektory. Grafické zobrazenie vektorovej veličiny je možné znázorniť vektorom, t.j. orientovanou úsečkou. Začiatok orientovanej úsečky je pôsobiskom sily . V newtonovskej mechanike sú za sily považované len tie sily, ktoré majú materiálny pôvod, t.j. ich pôvod je v existencii istého materiálneho objektu, resp. viacerých materiálnych objektov a v ich vzájomnom pôsobení. Tieto sily tiež nazývame skutočné (reálne). Vystupujú v rovniciach popisujúcich pohyb vzhľadom na inerciálnu vzťažnú sústavu. Možno ich rozdeliť na sily:
· vznikajúce pri priamom kontakte telies (tlakové sily, ťahové sily, sily trenia);
· vznikajúce pri vzájomnom pôsobení veľkého počtu molekúl (sily pružnosti);
· sprostredkované poľom (gravitačné sily, elektromagnetické sily).
Všetky dodnes známe sily v prírode, pôsobiace medzi hmotnými objektmi, sú dôsledkom základných fyzikálnych interakcií, s ktorými je spojená existencia základných druhov síl: gravitačné, elektromagnetické a jadrové. Jednotlivé interakcie, ich relatívnu silu a kvantum poľa, ktoré interakciu sprostredkováva udáva tabuľke 1.
Tab. 1 Základné fyzikálne interakcie
|
Základné fyzikálne interakcie |
|||
|
Typ |
Relatívna sila |
Oblasť pôsobenia [m] |
Častice poľa |
|
silná |
1 |
10-15 krátkodosahové |
gluóny |
|
elektromagnetická |
10-2 |
¥ ďalekodosahové |
fotóny |
|
slabé |
10-13 |
10-18 krátkodosahové |
bozóny |
|
gravitačné |
10-38 |
¥ ďalekodosahové |
? gravitóny |
Z tabuľky vidíme, že najsilnejšou základnou fyzikálnou interakciou je silná interakcia, ktoré sa uplatňujú medzi nukleónmi v jadre atómu. Silné interakcie sú zodpovedné za súdržnosť jadra a pôsobia len vo vnútri jadra, t.j. vo vzdialenosti polomeru jadra. Silná interakcia sa realizuje pomocou častíc s názvom gluóny.
Vieme, že v prírode sa vyskytujú rádioaktívne látky. Za ich rozpad sú práve zodpovedné slabé interakcie a častice s názvom bozóny. Prejavom pôsobenia slabej interakcie je vznik rádioaktívneho žiarenia. Spoločný názov pre silné a slabé interakcie je „ jadrové sily“. Jadrové sily sú silami krátkeho dosahu.
Elektromagnetické interakcie sú približne sto krát slabšie ako silné interakcie. Pôsobia medzi elektricky nabitými telesami, medzi prúdovodičmi, ktorými preteká prúd a i. Interakcia sa uskutočňuje prostredníctvom kvánt elektromagnetického poľa, ktorými sú fotóny. Sú zodpovedné za súdržnosť atómov a molekúl, resp. za stavbu látok. Sú to sily dlhého dosahu .
Najslabšej základnej interakcii odpovedajú gravitačné sily. Sú to sily, ktorými pôsobí planéta na telesá na jej povrchu. Týmito silami sú viazané Slnko a ostatné planéty našej slnečnej sústavy. Gravitačné sily sa realizujú prostredníctvom gravitačného poľa, ktoré obklopuje každý materiálny objekt. Predpokladá sa, že interakcia by sa mala realizovať prostredníctvom častíc - gravitónov. Doteraz však experimentálne neboli potvrdené. Gravitačné sily, sú silami dlhého dosahu.
S jednotlivými silami sa budeme zaoberať podrobnejšie v ďalších častiach. Okrem skutočných síl pôsobiacich v inerciálnych sústavách, sa stretávame s pojmom sila zdanlivá resp. fiktívna. Vyskytujú sa pri skúmaní pohybu v neinerciálnych sústavách, v ktorých okrem reálnych síl vystupujú výrazy s fyzikálnym rozmerom sily, ktoré zahrňujeme pod spoločný názov zotrvačné sily. (Pozn.: V súčasnom poňatí všeobecnej teórie relativity sa však tieto zotrvačné sily považujú práve tak za reálne ako tzv. skutočné sily.)
·
Moment sily
a)
Moment sily vzhľadom na bod
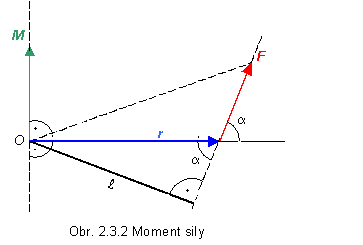
Vektorová fyzikálna veličina moment sily M vzhľadom na zvolený bod O je určená vektorovým súčinom polohového vektora r pôsobiska sily F vedeného z bodu O a tejto sily F (obr. 2.3.2) (Pozn.: Pozor na poradie vektorov, pretože vektorový súčin nie je komutatívny.)
M = r ´ F (2.3.4)
Moment sily M je teda vektor, ktorý má veľkosť rovnú ploche rovnobežníka určeného vektormi r a F , resp. súčinu rFsin a , kde a je uhol, ktorý zvierajú vektory r a F. Moment sily je vektor so začiatkom v bode O, kolmý na rovinu určenú vektormi r a F a smeruje do tej polroviny, že vektory r, F a M vytvárajú pravotočivý systém. Moment sily vzhľadom na daný bodu sa nezmení, ak tento bod posunieme do ľubovolného bodu jej vektorovej priamky.
Veľkosť momentu
sily M možno vyjadriť pomocou vzdialenosti vektorovej priamky sily F , ktoré sa nazýva tiež rameno
sily l , určené rovnicou l = r sin a
M = | r ´ F | = r F sin a = F r sin a = F l (2.3.5)
Ak pôsobiaca
sila je nenulová , F ¹ 0 a moment sily M = 0, znamená to, že bod O leží
na vektorovej priamke vektora F a
uhol a = 0.
Moment sily je mierou otáčavého
účinku sily vzhľadom na zvolený bod O.
Jednotkou momentu sily je newton meter,
N.m = kg.m2.s-2
_____________________________________
Príklad 2.3.1
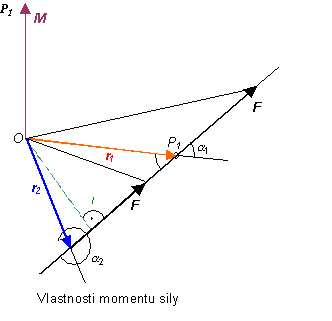
Ukážte, že moment sily M sa nezmení pri ľubovolnom posunutí pôsobiska sily F do ľubovolného bodu jej vektorovej priamky.
Riešenie: Pre veľkosť
momentu sily M1
s pôsobiskom sily F v bode P1 podľa obrázka platí
M1 = | r1 ´ F | = r1 F sin
a1 = F l
Ak je pôsobisko sily F v bode P2
,
M2 = | r2 ´ F | = r2 F sin a2 = F l
Pravé strany
posledných dvoch rovníc sa
rovnajú, potom porovnaním ľavých strán rovníc dostávame M1
= M2. Pretože vektory F, r1 , r2 ležia v tej istej rovine pre
ľubovolné dva body vektorovej priamky sily F platí M1 = M2.
______________________________________________________________
b) Moment sily vzhľadom na os
Moment sily vzhľadom na os prechádzajúcej ľubovolným bodom O je definovaný ako priemet momentu sily vzhľadom na zvolený bod O do tejto priamky. Uvažujme priamku p a príslušný moment Mp. Vektory r a F zapíšeme v tvare
r = r|| + r^![]() F = F|| + F^
F = F|| + F^![]()
kde r^![]() je zložka vektora r kolmá na priamku p a r|| je zložka rovnobežná s priamkou p. Rovnako i zložky vektora F sme rozložili na zložku rovnobežnú a kolmú s danou priamkou p. Moment sily vzhľadom
na ľubovolný bod priamky p je
je zložka vektora r kolmá na priamku p a r|| je zložka rovnobežná s priamkou p. Rovnako i zložky vektora F sme rozložili na zložku rovnobežnú a kolmú s danou priamkou p. Moment sily vzhľadom
na ľubovolný bod priamky p je
M = r
´ F = ( r|| + r^ ) ´
( F|| + F^) = r||
´ F|| + r^ ´ F|| + r||
´ F^+
r^´ F^![]()
Keďže vektory r|| a F||
sú kolineárne, vektorový
súčin je nulový. To isté platí pre
vektorový súčin r^ ´ F^![]() = 0
= 0
M = r^ ´ F|| + r||
´ F^
= M||
+ M^
Na základe fyzikálneho významu skalárneho súčinu môžeme moment sily vzhľadom na priamku p, ktorá je určená jednotkovým smerovým vektorom r určiť
Mr = ( M.r) r (2.3.6)
S využitím momentu sily vzhľadom na priamku resp. vzhľadom na os, sa stretneme pri skúmaní rotačného pohybu tuhého telesa.
Kontrolné otázky k časti 2.3.1
1. Čo je predmetom štúdia dynamiky?
2. Kedy hovoríme o tzv. newtonovskej mechanike resp. o dynamike klasickej nerelativistickej mechaniky?
3. Zadefinujte pojem izolovaná vzťažná sústava a napíšte matematické vyjadrenie tejto skutočnosti.
4. Definujte inerciálnu vzťažnú sústavu. Uveďte príklady takýchto sústav.
5. Je sústava pevne spojená so Zemou inerciálna? Za akých podmienok ju musíme považovať za neinerciálnu sústavu?
6. Ktorá veličina patrí medzi najvýznamnejšie dynamické charakteristiky telies?
7. Definujte minimálne 5 základných veličín, s ktorými sa pracuje v dynamike.
8. Definujte hybnosť hmotného bodu, napíšte matematické vyjadrenie pre hybnosť hmotného bodu a objasnite význam jednotlivých veličín.
9. Pri dokonale pružnom náraze hmotného bodu na stenu, zmení sa rýchlosť hmotného bodu po náraze? Aká bude zmena jeho hybnosti?
10. Je jednotkou hybnosti v SI sústave kg.m.s.?
11. Definujte veličinu moment hybnosti hmotného bodu , napíšte jej matematické vyjadrenie, určite jej smer a rozmer v SI sústave.
12. Definujte pojem sila a napíšte jej rozmer pomocou základných jednotiek sústavy SI.
13. Uveďte, s ktorými fundamentálnymi silami sa v prírode stretávame.
14. Uveďte, ktoré sily sú krátkeho dosahu a ktoré sú ďalekého dosahu.
15. Definujte veličinu moment sily a vysvetlite jej fyzikálny význam.
16. Aká veličina určuje mieru otáčavého účinku sily? Napíšte jej rozmer.
17. Vysvetlite, za akých podmienok môže byť moment sily M = 0
18. Vysvetlite fyzikálny význam rovnice Mr = ( M.r) r, kde M je moment sily a r
jednotkový vektor priamky p.