2.3.8 Práca,  energia ,  výkon    

 

·       Práca

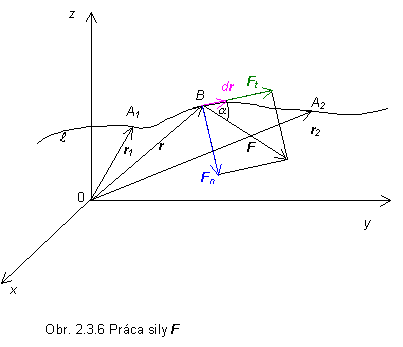
Nech pôsobením sily F na hmotný bod sa tento hmotný bod posunie po určitej dráhe z bodu A1 o polohovom vektore r1 do bodu A2 o polohovom vektore r2 . V  tomto prípade hovoríme o dráhovom účinku sily, resp. o práci sily F po  uvažovanej krivke ( obr. 2.3.6), ktorú možno vyjadriť pomocou  vzťahu

 

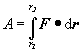                                                                                                                      (2.3.38)

    

     Z uvedeného vzťahu vidíme, že práca sily F závisí nielen od pôsobiacej sily,  od počiatočného   a  koncového bodu trajektórie, po ktorej sa pôsobisko sily pohybuje, ale aj na vzájomnej orientácii vektora sily F a vektora posunutia dr.

    Práca je skalárna fyzikálna veličina. Jednotkou práce v sústave SI je 1 J ( joule).  1 J = 1 N.m = 1 kg.m2.s-2. Joule (1 J) je práca , ktorú vykoná konštantná sila 1 N pôsobiaca po dráhe 1 m v smere sily. V molekulovej a atómovej fyzike sa používa často jednotka 1 eV (elektronvolt), 1 eV = 1,602. 10-19 J. V elektrotechnike sa stretávame s ďalšou jednotkou práce 1 kWh  (kilowatthodina), ktorá vyplýva z definície výkonu (pozri nasledujúcu časť Výkon ). 1 kWh = 3,6. 106 J

 

            Vo všeobecnosti sila  počas pohybu môže meniť svoju veľkosť i smer. Pri elementárnom posunutí dr možno silu F považovať za konštantnú. Prácu pri elementárnom posunutí nazývame  elementárnou  prácou  a jej veľkosť možno určiť vzťahom

 

                                                                                   (2.3.39)

 

Práca sily bude nulová v prípadoch ak:

1)     F = 0 alebo dr = 0

2)     F·dr  = 0 t.j. ak pôsobiaca sila a elementárne posunutie sú navzájom kolmé vektory.

 

Rozložme pôsobiacu silu v ľubovolnom bode trajektórie na zložku Ft  - rovnobežnú s elementárnym posunutím dr   a na zložku Fn  kolmú na smer posunutia. Dráha bodu môže byť určená väzbou,  napríklad podložkou.  Sila Fn  sa ruší silou,  ktorou pôsobí podložka na hmotný bod. Za predpokladu, že máme určenú silu  i trajektóriu možno vyjadriť prácu vzťahom

 

  

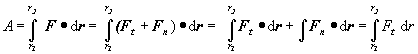                                  (2.3.40)

 

Rovnica (2.3.40) vyjadruje skutočnosť, že ak smer sily a dráhy nie je rovnaký, prácu koná len zložka sily v smere dráhy. Túto skutočnosť  možno vyjadriť i rovnicou

 

 

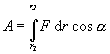                                                                                                               (2.3.41)

 

kde a  je uhol, ktorý zviera smer  vektor sily s vektorom posunutia. Ak vektor sily je konštantný, t.j. F = konst., v tomto prípade nezávisí práca na tvare dráhy, nakoľko z rovnice (2.3.38) dostávame

 

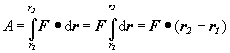                                                                                (2.3.42)

Prácu konštantnej sily po úsečke dĺžky l (l-dĺžka trajektórie medzi počiatočným bodom A a koncovým bodom B) je daná súčinom priemetu sily do smeru úsečky a dĺžky úsečky, nakoľko

 

 

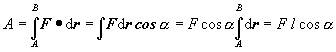
Príklad 2.3. 11  Vyjadrite tiažovej sily pri posunutí jej pôsobiska z bodu A o y –ovej súradnici yA  do bodu B o y –ovej súradnici yB.

 

Riešenie: V karteziánskej súradnicovej sústave so zvislou  y –ovou osou vyjadríme si  vektor tiažovej sily FG = -m g j a vektor posunutia dr  =dx i+ dy j +dz k, ktoré dosadíme do vzťahu (2.3.38).

 

 

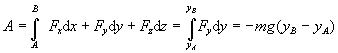
Z posledného výrazu vyplýva, že práca tiažovej sily závisí len od počiatočnej a konečnej y-ovej súradnice trajektórie  a nezávisí na tvare trajektórie.  V prípade, že hmotný bod: znižuje svoju výšku                           yA   > yB        A > 0    t.j. práca tiažovej sily je kladná

zvyšuje svoju výšku                           yA   < yB        A  < 0   t.j. práca tiažovej sily je záporná

nezmení svoju výšku pri premiestnení    yA  = yB        A  = 0   t.j. tiažovej sily nekoná  prácu.

–––––––––––––––––––––––––––

Ak práca sily nezávisí na trajektórii, ale len na počiatočnom a koncovom bode trajektórie, nazývame túto silu konzervatívnou. Práca konzervatívnych síl po uzavretej krivke je nulová.

Príkladom konzervatívnych síl sú sila tiažová a sila gravitačná.  V prípade, že práca sily závisí na trajektórii, hovoríme o silách nekonzervatívnych resp. disipatívnych. Príkladom disipatívnych síl je sila trenia a sila odporu prostredia.

 

·       Kinetická energia

Zo skúsenosti vieme, že ak pohybujúci  objekt zmenil svoju rýchlosť vzhľadom k zvolenej inerciálnej sústave, musela byť vykonaná práca iným telesom. Hovoríme, že práca na objekte bola vykonaná inou silou,  výsledkom ktorej je zmena pohybu objektu.  Dynamická veličina, ktorá súvisí s pohybom a ktorá sa v dôsledku vykonania práce zmenila sa nazýva kinetickou energiou. Objekt taktiež môže opačne na úkor kinetickej energie konať prácu. Vzťah medzi prácou vykonanou na objekte a kinetickou energiou možno odvodiť z druhého pohybového zákona (2.3.8):

 Nech hmotný bod  o  hmotnosti m, nachádzajúci sa v časovom okamihu t1  v mieste A1 s polohovým vektorom r1 má rýchlosť v1 a v časovom okamihu t2   sa nachádza v mieste A2 s polohovým vektorom r1   a má rýchlosť v2  . Pohybová rovnica  hmotného bodu, na ktorý  pôsobí celková sila F, je

 

 

 

Ak  celú  rovnicu vynásobíme skalárne vektorom posunutia dr  a zintegrujeme pozdĺž trajektórie z bodu A1 do bodu A2 získame výraz pre prácu , ktorú vykonala výsledná sila pri premiestnení objektu z bodu A1 do bodu A2:

 

 

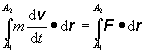
Keďže skalárny súčin je komutatívny,   platí

 

 

Deriváciou rovnice   možno ukázať , že platí . Po dosadení uvedených vzťahov do pravej strany rovnice dostaneme

 

   

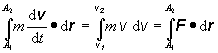
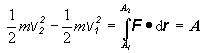                                                                                       (2.3.43)

 

Prácu sily F možno vyjadriť ako prírastok výrazu mv2 /2, ktorý nazývame kinetickou energiou

 

                                                                                                                     (2.3.44)

 

Na základe rovnice (2.3.44) možno prácu sily F (2.3.43) vyjadriť ako prírastok kinetickej energie, t.j. rozdielom kinetickej energie v konečnom stave a kinetickej energie v počiatočnom stave

 

 

                                                                                                                        (2.3.45)

 

Rovnicu  (2.3.45), resp (2.3.43) nazývame veta o kinetickej energii pre hmotný bod, alebo teoréma práce, ktorá hovorí: Zmena kinetickej energie hmotného bodu sa rovná práci vykonanej výslednicou pôsobiacich síl pri premiestnení hmotného bodu z počiatočnej polohy do konečnej polohy. Táto veta sa často využíva pri riešení príkladov, kedy máme určiť rýchlosť bodu v určitom mieste trajektórie, alebo keď rýchlosť v určitom bode je známe a máme určiť iný parameter trajektórie.

Súvislosť medzi kinetickou energiou a hybnosťou v klasickej newtonovskej mechanike určuje rovnica

 

                                                                        (2.3.46)

 

kde p1, resp. p2  je veľkosť počiatočnej a konečnej hybnosti hmotného bodu hybnosti hmotného bodu.

Jednotkou kinetickej energie v sústave SI je  rovnako ako pre prácu 1 J = 1 N.m = 1 kg. m2. s-2

 

·       Potenciálna energia               

 

Okrem kinetickej energie sa stretávame so skalárnou  fyzikálnou veličinou potenciálna energia. Tento pojem možno objasniť nasledovným experimentom: Na lane, prevesenom cez pevnú  kladku, máme zavesené dve rovnaké kocky o hmotnosti m (obr.    2.3.8) , pričom kocku (1) držíme položenú na zemi. Ak kocku  (1) pustíme a udelíme jej smerom nahor určitú počiatočnú rýchlosť,  pri pohybe kladky bez trenia sa kocka posunie do výšky h2 , v okamihu, keď kocka (2) dopadne na zem.

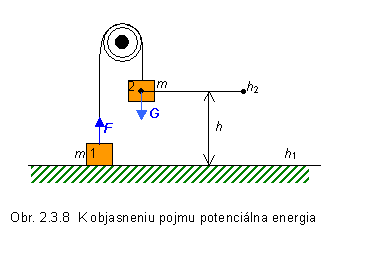
Sila F, ktorou prostredníctvom lana pôsobí druhá kocka na prvú je vlastne tiaž G druhej kocky prenesená lanom na prvú kocku.  Takže pre veľkosti síl  platí

 

     F = G = mg                                                                                                                 (2.3.47)

 

Pri posune prvej kocky sila F  vykoná prácu

 

     A = F h = Gh2 = mgh2                                                                                                (2.3.48)

 

ktorá je však rovnaká ako práca tiažovej sily G pri pohybe druhej kocky smerom nadol. Prvá kocka konala prácu, pretože druhá kocka padala nadol z určitej výšky nad zemou. Schopnosť konať prácu úzko súvisí s polohou kocky (resp. ľubovoľného telesa. ) Hovoríme , že kocka má potenciálnu  energiu Ep.  Potenciálna energia je skalárna veličina, ktorej veľkosť sa rovná práci, ktorú tiaž kocky (resp.  telesa) vykoná pri páde z danej polohy h2  do určitej polohy h1, vzhľadom na ktorú potenciálnu energiu vzťahujeme. V našom prípade h1 sme zvolili za referenčnú polohu, t.j. h1 = 0 . Pri  malých výškach nad zemou pre potenciálnu energiu platí vzťah

 

Ep  = mgh2                                                                                                                        (2.3.49)

 

Treba si uvedomiť, že fyzikálny zmysel má iba rozdiel potenciálnej energie medzi dvomi polohami skúmaného  hmotného bodu (telesa). V nami zvolenom prípade platí pre prácu, ktorú koná pôsobisko tiaže rovnica

 

A = Ep2  -  Ep1 = mg( h2   - h1)                                                                                            (2.3.50)

 

Vo všeobecnosti, systém, v ktorom všetky sily sú konzervatívne definujeme ako konzervatívny systém. (Pod systémom budeme rozumieť teleso, ktorého pohyb skúmame a časti okolia telesa, na ktoré naň pôsobia. V našom prípade kocky a Zem.) Práca konzervatívnych síl nezávisí od trajektórie. V konzervatívnom systéme definujeme veličinu potenciálnej energie Ep  :

Práca vykonaná v konzervatívnom systéme sa rovná úbytku potenciálnej energie systému Ep,, čo možno zapísať vzťahom

 

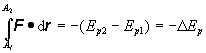                                                                                    (2.3.51)

 

Je vhodné si uvedomiť, že práca tiaže (resp. každej vonkajšej  sily, pre ktorú možno definovať potenciálnu energiu) sa rovná poklesu potenciálnej energie. V prípade kinetickej energie sme zistili, že práca výslednej sily sa rovná prírastku kinetickej energie  (rovnica 2.3.45). Podrobnejšie sa s potenciálnou energiou ešte budeme zaoberať v časti 2.5.

 

·       Celková mechanická energia

 

Súčet kinetickej a potenciálnej energie  nazývame celkovou mechanickou energiou,  pre ktorú platí

 

E = Ek + Ep                                                                                                               (2.3.52)

 

V konzervatívnych systémoch platí zákon zachovania mechanickej energie:  Súčet kinetickej a potenciálnej energie v ľubovolných dvoch stavoch konzervatívneho systému je rovnaký, t.j. mechanická energia v konzervatívnych systémoch sa zachováva. Podrobnejšie sa problematike potenciálnej energie a zákonu zachovania celkovej mechanickej energie  venujeme v nasledujúcej časti  2.5.7.

 

·       Výkon

Práca vykonaná za jednotku času určuje skalárnu fyzikálnu veličinu, ktorú nazývame výkon. Priemerný výkon určuje podiel práce vykonanej za časový interval Dt a tento časový interval Dt

 

                                                                                                                       (2.3.53)

 

Okamžitý výkon určuje vzťah

 

                                                                                                     (2.3.54)

 

Jednotkou výkonu v sústave SI je kg.m2.s-3 , ktorá sa nazýva watt (W). Keďže platí

 

1 W = 1 J . 1 s-1

 

výkon 1 W má zariadenie, ktoré vykoná prácu 1 J za 1 s. Iné vyjadrenie pre výkon P cez silu  F pôsobiacu na hmotný bod a okamžitú rýchlosť  v pohybu pôsobiska sily, získame po dosadení vzťahu (2.3.39) za prácu

 

                                                                                           (2.3.55)

 

Ak poznáme výkon  ako funkciu času, t.j. P = P(t), možno celkovú  prácu  za časový interval Dt = t2 – t1  vyjadriť  vzťahom

 

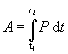                                                                                                                   (2.3.56)

 

·                 Účinnosť

Pomer užitočného (získaného) výkonu (P) ku dodávanému výkonu, t.j. k  príkonu Pp nazývame účinnosťou zariadenia.h

 

                                                                                                                      (2.3.57)

 

resp. pre  jej vyjadrenie v %

 

                                                                                                             (2.3.58)

 

Účinnosť reálneho zariadenia je vždy menšia ako jedna, pretože žiadne zariadenie nepracuje bez energetických strát.

 

Kontrolné otázky k časti 2.3.8

 

1.     Definujte pojem práca a matematicky ju zapíšte.

2.     Napíšte jednotku práce v sústave SI.

3.     Aké účinky sily poznáme?

4.     Vysvetlite kedy je vykonaná práca maximálna a kedy minimálna?  Ktorá zložka sily koná prácu?

5.     Otec i malý syn ťahajú rovnakou silou, po rovnakej dráhe každý svoje rovnaké sánky. Narobia sa rovnako? Svoju odpoveď matematicky zdôvodnite.

6.     Definujte  stredný a okamžitý výkon a určite jeho jednotku pomocou  základných jednotiek sústavy SI.

7.     Vysvetlite súvis medzi prácou a kinetickou energiou hmotného bodu.

8.     Kedy bude mať teleso pri dopade na zem väčšiu rýchlosť: ak padá z výšky h voľným pádom, alebo keď sa pohybuje bez trenia po naklonenej rovine z rovnakej výšky?

9.     Dve rovnaké telesá sa pohybujú  po dvoch naklonených rovinách s rôznymi  uhlami sklonu  z rovnakej výšky. Čo možno povedať o rýchlostiach telesa pri dopade na zem  v obidvoch prípadoch?

10.  Tlstý chlapec a chudý chlapec sa šmýkajú bez trenia po rovnakej šmýkačke.  Ktorý z nich dosiahne väčšiu rýchlosť pri dopade?

11.  Definujte pojem „ potenciálna energia“. Určite jej rozmer a vysvetlite jej fyzikálny význam.

12.  Rozhodnite, či pri pohybe skúmaného hmotného bodu (telesa)  po naklonenej rovine do výšky h treba taká istá sila ako pri zdvíhaní toho istého telesa do tej istej výšky. Svoje tvrdenie matematicky zdôvodnite.

Definujte pojem „celková mechanickej energia“.