2.3.6 Silové
pôsobenie pri vybraných pohyboch
V nasledujúcej časti prediskutujeme niektoré druhy síl, s ktorými sa často stretávame v inerciálnych vzťažných sústavách.
· Dostredivá sila
Ak rozkrútime kameň upevnený na lane tak, že sa pohybuje rovnomerným pohybom, cítime, že na to je potrebné svalové napätie. Prečo je potrebná sila, keď sa teleso pohybuje po kružnici rovnomerne? Pravde nie priamočiaro. Z kinematiky vieme, že táto sila je potrebná, aby sme vychýlili teleso z priamočiarej dráhy, po ktorej sa snaží teleso zotrvačnosťou pohybovať . Sila je potrebná na to, aby sme vytvorili dostredivé zrýchlenie v2/r. Na základe 2. Newtonovho zákona pôsobí na hmotný bod sila, ktorá je orientovaná vždy do stredu kružnice a nazývame ju dostredivou silou. Jej matematické vyjadrenie je dané rovnicou
![]() (2.3.28)
(2.3.28)
kde r je polomer kružnice po ktorej sa hmotný bod s hmotnosťou m pohybuje a r je jednotkový vektor so začiatkom v strede kružnice. Dostredivá sila je silou od väzby pre hmotný bod pohybujúci sa nie priamočiaro. Z kinematiky vieme, že táto sila je potrebná na zakrivenie trajektórie. V prípade rovnomerného pohybu po kružnici je sila od väzby vždy kolmá v danom bode väzby k dotyčnici ku kružnici. Vektor rýchlosti má v tomto prípade smer dotyčnice ku kružnici, takže možno povedať, že dostredivá sila je vždy kolmá na vektor rýchlosti.
Roztočme napr. sklenenú vianočnú guľu upevnenú na niti, ktorú držíme pevne v ruke tak, že vo vertikálnej rovine koná rovnomerný pohyb po kružnici. Úlohu dostredivej sily hrá v tomto prípade ťahová sila nite. Sila ťahá guľu, guľa ťahá niť. Tieto dve sily sú sily akcie a reakcie. Silu, ktorou guľa pôsobí na niť, často nazývame odstredivou. Táto sila vzniká ako reakcia na silu dostredivú. Uvedené výsledky platia aj pre prípad, keď úlohu „nite“ preberá príťažlivá sila. Pohyb Mesiaca okolo Zeme možno považovať za rovnomerný pohyb po kružnici. Čo udržuje Mesiac na danej dráhe? Zem udržuje Mesiac „neviditeľným lanom“- príťažlivou silou. Gravitačná príťažlivá sila je dostredivou silou, ktorou Zem pôsobí na Mesiac. Dostredivou silou môže byť ako ťahová, tak gravitačná sila, ale i sila iného pôvodu. Ozrejmime si to na dvoch prípadoch: pohybu auta v zákrute a pohyb družice na obežnej dráhe okolo Zeme.
1) Pohybu auta v zákrute : V strede batožinového priestoru auta, ktoré sa pohybuje po rovnej ceste značnou rýchlosťou, máme voľne uložený kartón vajíčok na hladkej podložke. Čo sa stane, ak náhle auto vojde do ľavotočivej zákruty, pričom pohyb v zákrute budeme považovať za rovnomerný pohyb po kružnici?
Kartón s vajíčkami sa posunie po podložke batožinového priestoru smerom vpravo a je pri veľkej rýchlosti pritisnutý na vnútornú stenu batožinového priestoru. (Pri istých rýchlostiach sa o tom možno presvedčiť škvrnou z rozbitých vajíčok.) Rozoberme si, čo sa vlastne deje: Pohyb auta v zákrute možno považovať za rovnomerný pohyb po kružnici. Dostredivou silou, ktorá spôsobuje tento pohyb, je trecia sila, ktorou pôsobí povrch vozovky na pneumatiky auta. Táto sila smeruje pozdĺž polomeru do stredu zákruty a je určená vzťahom (2.3.28) . Je rozložená na všetky štyri kolesá.
Kartón s vajíčkami by konal tiež rovnomerný pohyb po kružnici, keby sila trenia, ktorou podložka batožinového priestoru na kartón pôsobí bola dostatočne veliká. V tom prípade by krabica zotrvala na pôvodnom mieste. V prípade hladkej podložky, kartón sa posunie po batožinovom priestore. Kartón s vajíčkami z hľadiska vzťažnej sústavy pevne spojenej so Zemou pokračuje v priamočiarom pohybe, zatiaľ čo podložka pod ním sa posúva, pokiaľ kartón nenarazí na vnútornú stenu. Tlaková sila steny na kartón realizuje dostredivú silu a kartón sa začne pohybovať rovnomerne po kružnici spolu s autom.
2) Pohyb družice na obežnej dráhe okolo Zeme.
Predstavme
si, že kartón s vajíčkami by sme umiestnili do družice, ktorá obieha okolo
Zemi a nachádza sa v beztiažovom stave. Dostredivá sila, ktorá
udržuje družicu, i všetko
v nej, v rovnomernom pohybe po kružnici, je príťažlivá gravitačná
sila, ktorou Zem pôsobí na družicu
i na veci vo vnútri družice. Táto sila smeruje do stredu kružnice
po ktorej sa družica pohybuje, t.j. do stredu
Zeme a je určená vzťahom (2.3.28). Čo sa deje s kartónom
vajíčok? Ako v aute, tak
i v družici sa kartón
pohybuje rovnomerným pohybom po kružnici vplyvom dostredivej sily.
Zistili sme, že v aute sa kartón posunie k stene, ktorá pôsobí na
neho tlakovou silou. Z televíznych záznamov je známe, že
v obiehajúcej družici kozmonaut i veci plávajú a kozmonaut nepociťuje žiadnu pôsobiacu silu,
rovnako ako v prípade kartónu. Čo spôsobilo tento rozdiel? Je to
v dôsledku rôznej povahy dostredivej sily v uvedených príkladoch.
V aute je dostredivá sila sprostredkovaná priamym plošným kontaktom časti kartónu a steny batožinového priestoru –
jedná sa o plošnú silu, o ktorej pojednáme bližšie v nasledujúcom
odstavci. V obiehajúcej
družici dostredivá sila má charakter objemovej
sily. Je to príťažlivá gravitačná sila, ktorá
je výslednicou elementárnych síl pôsobiacich na objemové elementy jednotlivých
častí družice a vecí vo vnútri úmerne ich hmotnostiam. Nedochádza
k žiadnemu plošnému stlačovaniu.
Kontaktná sila
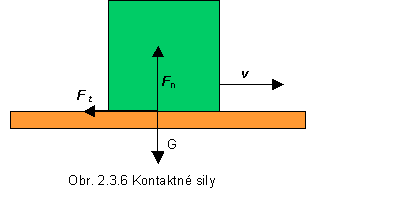
Pri styku dvoch telies na dotykových plochách v dôsledku zložitých procesov interakcie atómov a molekúl dotýkajúcich sa povrchov hmotných objektov vzniká tzv. kontaktná sila. Na teleso položené na rovinnej podložke pôsobí zvisle nadol sila - tiaž telesa G. Podľa zákona akcie a reakcie na teleso bude zvisle nahor pôsobiť sila reakcia podložky Fn, ktorú nazývame normálová kontaktná sila Fn,. Normálová kontaktná sila (obr. 2.3.6) je kolmá na dotykovú rovinu pričom musí platiť podmienka rovnováhy síl
Fn + G = 0 (2.3.29)
Kontaknú silu môžeme zmerať napr. pri šmýkaní telesa po povrchu druhého telesa, kedy v smere dotyčnice k dotykovej rovine vznikne sila trenia Ft. Vzniká vonkajšie trenie,. Sily vonkajšieho trenia vznikajú medzi pevnými telesami, ktoré sa navzájom dotýkajú a sú k sebe pritlačované určitou silou. Ak teleso je v pokoji hovoríme o statickom trení. Ani jedna z kontaktných síl, (sila trenia a reakcia podložky), samostatne nemôžu zmeniť pohybový stav telesa.
Ak trenie vzniká pri pohybe jedného telesa po druhom, ktorého sa dotýka, hovoríme o dynamickom trení. Vonkajšie dynamické trenie sa prejavuje silami pôsobiacimi proti smeru vzájomného premiestnenia telesa. Má vždy smer opačný, ako je smer okamžitej rýchlosti. Pri vonkajšom trení rozlišujeme šmykové trenie a odpor proti valeniu. Ak sú dotýkajúce sa povrchy suché, hovoríme o suchom trení. Ak je medzi nimi vrstva viskóznej látky, hovoríme o viskóznom trení. Ak je plocha dotyku telies rovinná plocha, používa sa pri približných výpočtoch Amontov zákon. Pri suchom trení, podľa Amonta, veľkosť trecej sily Ft nezávisí na obsahu tejto plochy, ale je priamoúmerná veľkosti Fn normálovej zložky sily Fn (tlakovej sily) pôsobiacej na pohybujúce sa teleso, ktorou je toto teleso pritlačované k druhému telesu.
Ft= m Fn (2.3.30)
Konštanta m sa nazýva koeficient trenia. Rozlišujeme dve sily trenia: sila statického trenia a sily kinetického trenia a s tým i rozoznávame koeficient statického trenia ms a koeficient kinetického trenia mk.. Silu statického trenia si možno ozrejmiť pomocou nasledovného experimentu:
Po horizontálnej rovine začneme ťahať kváder malou silou F, ktorá je rovnobežná s horizontálnou rovinou. Kváder, napriek pôsobeniu malej sily, svoju počiatočnú polohu nezmení. Je to spôsobené drsnosťou dotykových plôch obidvoch materiálnych objektov. Tieto nerovnosti povrchu (existujú aj pri dôslednom opracovávaní materiálu) bránia posúvaniu jedného telesa po povrchu druhého. Ak silu F postupne zväčšujeme, pri istej jej veľkosti sa teleso dá do pohybu. Hraničnú hodnotu, ktorú musíme prekonať, aby sme teleso uviedli do pohybu, nazývame silou statického trenia Fts , pre ktorú v horizontálnom smere platí rovnosť Fts = F. Sila statického trenia zabraňuje šmýkaniu sa telesa po povrchu druhého telesa pokiaľ jej veľkosť spĺňa nerovnicu Fts £ ms Fn. . Koeficient ms závisí od materiálu, od jeho povrchovej úpravy jednotlivých stykových plôch (drsnosti, resp. hladkosti) a na rade iných vplyvov ako je napr. teplota. Prakticky nezávisí od veľkosti plochy vzájomného dotyku. Veľkosť sily statického trenia možno vyjadriť ekvivalentne vzťahom (2.3.30)
Fts = ms
Fn
Ak veľkosť pôsobiacej sily F prekročí hodnotu sily statického trenia, teleso sa dá do pohybu. Sila trenia sa zmenší. Ak teleso, za pôsobenia vlečnej sily F, sa šmýka po drsnej podložke konštantnou rýchlosťou v , podľa zákona akcie a reakcie pôsobí na teleso rovnako veľká, opačne orientovaná sila, nazývaná sila kinetického trenia Ftk, pre ktorú platí
F + Ftk
= 0
Aj pre silu kinetického trenia Ftk platí Amontov zákon, t.j.
Ftk = mk
Fn
V ideálnom prípade, kedy dotýkajúce sa plochy sú dokonale hladké, položíme koeficient trenia m = 0. Koeficient trenia m sa často vyjadruje pomocou uhla j, nazvaného uhol trenia. Pretože sily Ft a Fn sú navzájom kolmé, možno napísať
![]() (2.3.31)
(2.3.31)
j je teda uhol, ktorý zviera normálová sila Fn s výslednicou síl Fn + Ft . Tento uhol možno určiť jednoduchým spôsobom. Teleso položené na naklonenú rovinu, na ktoré pôsobí jeho vlastná tiaž G (obr. 2.3.7) sa po nej pohybuje posuvným pohybom s konštantnou rýchlosťou v, ak sa uhol, ktorý zviera táto rovina s vodorovnou rovinou, rovná práve uhlu j. Podmienka vzniku šmýkania telesa dolu naklonenou rovinou je
m s = tg jk (2.3.32)
pričom p/2 ³ j ³ j k
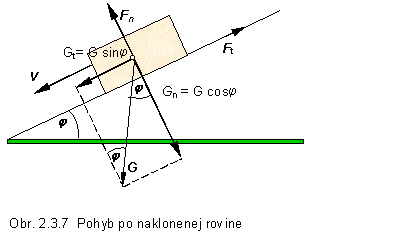
Pri odvodení tohto vzťahu vyjdime z pohybovej rovnice vo vektorovom tvare, kde výsledná sila je vektorovým súčtom tiažovej sily G a dvoch kontaktných síl, reakcie podložky Fn a sily trenia Ft.
ma = G + Fn +Ft (2.3.33)
Pri pohybe po naklonenej rovine rozložíme pôsobiace sily na zložky rovnobežné s naklonenou rovinou a na zložky kolmé na naklonenú rovinu:
G = [ G sin j, G cos j ] , Fn = [ 0, -Fn] F t = [ -F t ,0 ]
V smere rovnobežnom s naklonenou rovinou platí: ma = G sin j - Ft
V smere kolmom na naklonenú
rovinu platí: 0 = G cos j - Fn Þ Fn
= G cos j
Po dosadení za silu trenia, vzťah
(2.3.30) Ft = m
Fn = m G cos j,,
kde m je statický alebo kinetický koeficient trenia v závislosti od toho, či sa teleso už šmýka (m = mk) alebo sa pôsobením statického trenia nepohybuje (m = ms). V hraničnom prípade, kedy j = jk, je ešte zrýchlenie kvádra a = 0, takže z prvej rovnice po dosadení Ft dostaneme
![]() (2.3.34)
(2.3.34)
Meranie koeficientu kinetického
trenia sa zakladá na určení kritického uhla jk ,
pri ktorom sa teleso šmýka nadol po naklonenej rovine konštantnou rýchlosťou.
Kontrolné otázky k časti 2.3.6
1. Vysvetlite pojem dostredivá sila.
2. Chudý a tlstý cyklista vbiehajú do rovnakej zákruty, rovnakou rýchlosťou. Naklonia sa rovnako? Svoju odpoveď matematicky zdôvodnite.
3. Napíšte matematické vyjadrenie dostredivej sily.
4. Vysvetlite pojem odstredivá sila a napíšte jej matematické vyjadrenie.
5. Existujú kontaktné sily?
6. Platí zákon akcie a reakcie pre kontaktné sily?
7. Napíšte podmienku vzniku šmýkania telesa dolu naklonenou rovinou.
8. Aký význam majú sily trenia?
9. Vysvetlite pojem sila kinetického trenia Ftk a napíšte jej matematické vyjadrenie.
10. Kedy hovoríme a sile statického trenia a sile kinetického trenia?
11. Definujte koeficient trenia.
12. Závisí koeficient trenia od veľkosti plochy vzájomného dotyku?
13. Od akých parametrov závisí koeficient kinetického trenia?
14. Zapíšte podmienku rovnováhy síl.
15. Nakreslite rozklad pôsobiacich síl na naklonenej rovine v prípade, že silu trenia zanedbávame. Matematicky zapíšte pohybovú rovnicu pre Vami zvolený prípad.
16. Nakreslite rozklad pôsobiacich síl na naklonenej rovine v prípade, že silu trenia a silu odporu proti pohybu uvažujeme.