2.3.2  Newtonove pohybové zákony

            Základ newtonovskej mechaniky tvoria tri zákony, formulované Isaacom Newtonom v roku 1687  v diele Philosophiae Naturalis Principia Mathematica (Matematické princípy prírodnej filozofie) spolu s gravitačným zákonom. Newtonove zákony, sú zobecnením veľkého množstva empirických poznatkov, overených platnosťou z  nich vyplývajúcich  dôsledkov.

 

 Zákon zotrvačnosti  - 1. Newtonov pohybový zákon

 

Každé teleso zotrváva v pokoj,i alebo v rovnomernom priamočiarom pohybe, pokiaľ nie je nútené, pôsobením vonkajších síl, tento svoj pohybový stav zmeniť.

Tento zákon, nazývaný zákon zotrvačnosti, (objavil ho už Galileo Galilei),  platí pre hmotný bod, resp. pre hmotný stred telesa, nakoľko sa v ňom nehovorí nič o rotácii telesa. Zákon zotrvačnosti platí vzhľadom na pokoj, resp. pohyb,  určený v inerciálnej súradnicovej sústave.

 

Zákon sily - 2. Newtonov pohybový zákon

 

Časová zmena hybnosti telesa je priamoúmerná pôsobiacej sile a má s ňou rovnaký smer. Matematické vyjadrenie zákona sily je

 

                                                                                                                          (2.3.7)

 

kde  p  je hybnosť telesa (resp. hmotného bodu). V prípade skúmania pohybu objektov, ktoré sa skladajú z častíc (atómov a molekúl), ktorých hmotnosť nie je premenná veličina (m = konšt.), t.j. nezávisí od rýchlosti pohybujúceho sa objektu,  možno zákon sily prepísať do tvaru

 

                                                                                                 (2.3.8)

 

Pod silou F máme na mysli celkovú výslednú silu F pôsobiacu na daný hmotný bod.  V tejto forme zákon sily hovorí: Sila F, pôsobiaca na hmotný bod, je priamoúmerná súčinu hmotnosti m pohybujúceho sa telesa a zrýchlenia telesa a, ktoré táto sila telesu udeľuje.

Pozn.: Musíme si uvedomiť, že hmotnosť je konštantnou veličinou len v nerelativistickej mechanike. Teda v tých  prípadoch, keď sa skúmaný hmotný bod (teleso) pohybuje značne menšími rýchlosťami ako je rýchlosť svetla vo vákuu. Zrýchlenie hmotného bodu na základe zákona sily  možno vyjadriť

 

                                                                                                                                 (2.3.9)

 

Túto rovnicu možno fyzikálne interpretovať: V inerciálnych vzťažných sústavách sa zotrvačnosť telesa prejavuje tým, že ak na teleso o hmotnosti m pôsobí vonkajšia sila  F  nadobúda zrýchlenie telesa konečnú hodnotu. V prípade, ak na teleso nepôsobí žiadna sila, alebo  výslednica pôsobiacich síl je nulová, teleso zotrváva v stave pokoja, alebo v rovnomernom priamočiarom pohybe.

Na základe rovnice (2.3.9) už vieme  matematicky určiť, prečo ak na dve telesá o rôznej hmotnosti pôsobia rovnaké sily, teleso o menšej hmotnosti nadobudne väčšie zrýchlenie. Čiže na základe zákona sily, pri pôsobení rovnako veľkých síl, telesá nadobudnú tým menšie zrýchlenie, čím sú väčšie ich hmotnosti. Preto sa pre hmotnosť zaviedol, ako sme už uviedli, i pojem zotrvačná hmotnosť.

 

Zákon akcie a reakcie - 3. Newtonov pohybový zákon

 

Sily, ktorými na seba pôsobia dve telesá, majú vždy  rovnakú  veľkosť a opačný  smer.

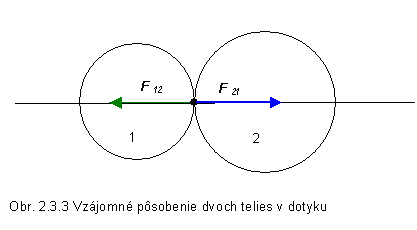
Sila F_{12 ,} ktorou pôsobí jedno teleso na druhé, sa nazýva akcia  a sila F₂₁ , ktorou pôsobí druhé teleso na prvé, sa potom nazýva reakcia. Podľa tretieho Newtonovho zákona platí v každom okamihu

 

F₁₂ = - F₂₁                                                                                                                 (2.3.10)

 

Sily, ktoré pôsobia na dve telesá, vždy vytvárajú dvojicu a pri viacerých telesách sily sú vždy párové. Nerozhoduje, ktorú zo síl nazveme akciu a ktorú reakciu.

Tretí Newtonov zákon tiež sa niekedy nazýva zákon vzájomného pôsobenia a možno ho formulovať: Každá akcia vyvoláva rovnako veľkú reakciu opačného smeru. Na základe tejto formulácie  je tento zákon známy ako zákon akcie a reakcie.  

Ako príklad možno uviesť zrážku dvoch telies, pri ktorej pôsobia tlakové sily vzájomného pôsobenia (obr. 2.3.3). Pri sledovaní jedného telesa musíme mať na zreteli, že sily akcie a reakcie sú silami pôsobiacimi na dve rôzne telesá a tieto sily nie je možné sčítať. Ak obidve telesá vytvárajú sústavu a hľadáme výslednicu vo vnútri tejto sústavy, potom tieto sily, splňujúce zákon akcie a reakcie, môžeme sčítať. Z tohto hľadiska zákon akcie a reakcie umožňuje prechod od dynamiky jedného hmotného bodu k dynamike sústavy hmotných bodov.

Z matematického zápisu zákona akcie a reakcie nevyplýva, že tieto dve sily ležia na jednej priamke. Presnejšiu túto skutočnosť  vystihuje zápis pomocou  momentu sily  M₂₁   = -  M₁₂

O podmienkach platnosti 3.Newtonovho zákona pojednáme v samostatnej časti 2.3.3.

 

_______________________________________

Príklad 2.3.2 Na základe vektorového počtu ukážte, že vektorová rovnica pre momenty síl vzhľadom na ľubovolný bod  M₂₁   = -  M₁₂  jednoznačne určuje  skutočnosť, že sily vzájomného pôsobenia F₁₂  a F₂₁ dvoch hmotných bodov s hmotnosťami m₁  a m₂  ležia na tej istej priamke.

Riešenie: Z predpokladu príkladu vyplýva, že  M₂₁   = -  M_{12  ,} čo možno  zapísať

 

 M₂₁   +  M₁₂ = 0                                                                                                                  (2.3.11)

 

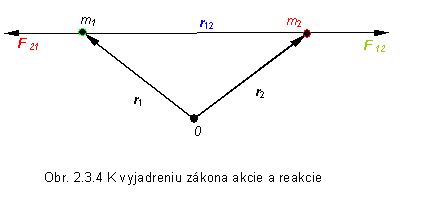
kde   M₂₁ = r₁ ´ F₂₁   a   M₁₂ = r₂ ´ F₁₂   , r₁  a   r₂ sú polohové vektory telies ( hmotných bodov) s hmotnosťami m₁  a m_{2 ,} F₁₂  je sila, ktorou pôsobí teleso s hmotnosťou  m₁ na teleso s hmotnosťou  m₂    a   F₂₁ je sila, ktorou pôsobí teleso s hmotnosťou  m₂ na teleso s hmotnosťou  m₁   (obr. 2.3.4) pre ktoré platí F₁₂ = - F₂₁

 

Po dosadení uvedených vzťahov do rovnice (2.3.11)  dostaneme

 

r₁ ´ F₂₁  + r₂ ´ F₁₂  =  - r₁ ´ F₁₂  + r₂ ´ F₁₂  =  (r₂ -  r₁) ´  F₁₂ = 0

 

Keďže obidva vektory z vektorového súčinu sú nenulové vektory, vektorový súčin je rovný nule, ak vektory (r₂ -  r₁)  a  F₁₂ sú rovnobežné. Vektor (r₂ -  r₁)  má smer spojnice hmotných bodov a teda i vektor F₁₂ leží na tejto spojnici . Obdobne z rovnice (2.3.11)  dostaneme

 

-(r₂ - r₁ ) ´ F₂₁ = 0                                                                                                                   (2.3.12)

 

Z rovnice (2.3.12), opäť z rovnakého dôvodu vyplýva, že  (r₂ -  r₁)  a  F₂₁ sú rovnobežné vektory a vektor F₁₂ leží na tejto spojnici hmotných bodov Þ že vektory F₁₂  a  F₂₁ ležia na tej istej priamke.

_______________________________________

 

Kontrolné otázky k časti 2.3.2

1.     Ak na dve telesá o rôznej hmotnosti pôsobia rovnaké sily, ktoré teleso nadobudne väčšie zrýchlenie?

2.     Napíšte základnú rovnicu určujúcu  pohyb hmotného bodu.

3.     Napíšte, čo je príčinou zmeny pohybového stavu skúmaného objektu.

4.     Vysvetlite, čím sa zaoberá dynamika hmotného bodu.

5.     Ktorá fyzikálne veličina je mierou zotrvačných a gravitačných vlastností telies?

6.      Definujte sústavu izolovanú a sústavu otvorenú.

7.     Čo je príčinou zrýchlenia hmotného bodu s hmotnosťou m nachádzajúceho sa v inerciálnej súradnicovej sústave?

8.       Napíšte aspoň tri druhy síl s účinkami ktorých ste sa už stretli. 

9.     Vyslovte a matematicky zapíšte Newtonove pohybové zákony.

 

10.  V akých vzťažných sústavách platia Newtonove pohybové zákony?

11.  Ak na hmotný bod v inerciálnej sústave pôsobí konštantná výsledná sila, aký pohyb koná hmotný bod?

12.  Napíšte základnú pohybovú rovnicu pre  teleso o hmotnosti m,  pohybujúce sa v inerciálnej sústave pod súčasným účinkom troch síl  F₁, F₂ a F₃.

13.  Definujte pojem hybnosť. Napíšte jej rozmer .

14.  Ak sa rýchlosť skúmaného objektu čo do veľkosti zmení na  trojnásobok začiatočnej hodnoty, napíšte o koľko sa zmení jeho hybnosť.

15.  V dôsledku pôsobenia sily  častica  jednotkovej hmotnosti sa  pohybuje tak, že veľkosť jej rýchlosti rastie kvadraticky s časom z nulovej hodnoty, pričom  konštanta  úmernosti  k = 1 m. s ^-3 . Nakreslite graf závislosti veľkosti pôsobiacej sily ako funkciu času.

16.  Napíšte matematický zápis, ktorý vyjadruje, že sila  akcie a reakcie ležia na jednej priamke.

17.  Vysvetlite princíp superpozície a napíšte jeho matematické vyjadrenie.

18.   Aká matematická rovnica vyjadruje ekvivalenciu medzi stavom kľudu a rovnomerným priamočiarym pohybom hmotného bodu?

19.  Ak výsledná sila pôsobiaca na hmotný bod v inerciálnej sústave je F  = konst., aký smer má vektor zrýchlenia?

20.    Ak výsledná sila pôsobiaca na hmotný bod v inerciálnej sústave je F  = konst.,  je smer vektora okamžitej rýchlosti  vždy rovnaký so smerom vektora sily?

21.  Uveďte príklad pôsobenia vonkajších síl, pri ktorom smer rýchlosti hmotného bodu nemá smer  pôsobiacej sily.

22.  Ak na hmotný bod  pôsobí súčasne viac síl, čím  je určený pohybový stav hmotného bodu?

23.  Pomocou rovnice zapíšte skutočnosť, že sily akcie a reakcie ležia na jednej priamke.