2.3.5 Pohybová
rovnica hmotného bodu a jej riešenie
Druhý pohybový zákon, určený rovnicou (2.3.8) F = ma, predstavuje vektorovú diferenciálnu rovnicu 2. rádu, ktorú tiež nazývame pohybovou rovnicou hmotného bodu (telesa). Pri zostavovaní pohybovej rovnice (2.3.8) musíme zvážiť všetky pôsobiace sily, t.j. F= [ Fx , Fy ,Fz] v rovnici znamená vektorový súčet všetkých pôsobiacich síl. Táto rovnica je ekvivalentná trom skalárnym rovniciam
![]()
![]()
![]() (2.3.17)
(2.3.17)
Pre jednoznačné vyriešenie týchto troch skalárnych diferenciálnych rovníc, resp. pre jednoznačné určenie pohybu hmotného bodu, potrebujeme poznať ešte doplňujúce údaje, určujúce hodnoty dvoch vektorových, alebo šiestich skalárnych konštánt. Tieto hodnoty sa nazývajú počiatočné podmienky. Obyčajne sa uvádzajú hodnoty polohového vektora a vektora rýchlosti v okamihu t = 0 na začiatku merania, t.j. r0 a v0.
Pohybový zákon môžeme využiť v dvoch smeroch.
· Ak poznáme hmotnosť telesa m, výslednú silu pôsobiacu na teleso F a počiatočné podmienky r0 a v 0 , môžeme určiť v každom časovom okamihu t jeho rýchlosť v a polohový vektor r.
·
Ak je známa hmotnosť hmotného bodu m
a závislosť r = r(t), možno
vyjadriť vzťah pre pôsobiacu silu.
Všeobecný spôsob riešenia pohybovej rovnice hmotného bodu v inerciálnej vzťažnej sústave si ukážeme na nasledovných troch prípadoch. Ak pôsobiaca sila má všetky tri zložky nenulové, riešili by sme tri skalárne rovnice pre odpovedajúce zložky sily. Pre jednoduchosť budeme uvažovať prípady, kedy pôsobiaca sila má smer osi x. t.j. F = [Fx, 0,0].
1/
Pôsobiaca sila je konštantná - Fx = konšt.
Pohybová rovnica (2.3.20) je
diferenciálna rovnica druhého rádu tvaru
![]()
Budeme ju riešiť znížením rádu diferenciálnej rovnice na prvý, t.j. najprv nájdeme riešenie pre rýchlosť:
![]() (2.3.18)
(2.3.18)
![]() (2.3.19)
(2.3.19)
Konštanty C1 a C2 v rovniciach (2.3.18) a (2.3.19) určíme z počiatočných podmienok v časovom okamihu t = 0 s, napríklad: teleso sa nachádzalo v pokoji a v začiatku súradnicovej sústavy t.j. x0 = 0 a v0 = 0
![]()
![]()
![]() (2.3.20)
(2.3.20)
![]() (2.3.21)
(2.3.21)
čím sme získali rovnice pre polohu (2.3.20) a rýchlosť (2.3.21) hmotného bodu pri rovnomerne zrýchlenom pohybe v danom časovom okamihu t. V špeciálnom prípade, keď Fx = 0 , dostaneme rovnice
vx = C1 x = C1t
+ C2
Pre zvolené počiatočné podmienky rovnice (2.3.21) a (2.3.20) prejdú na rovnice pre rovnomerný pohyb
vx =v0 , x = v0
t
2/ Pôsobiaca sila je funkciou času Fx
= Fx(t)
Pohybovú rovnicu (2.3.20) prepíšeme
na tvar
![]()
Po jej úprave a separácii premenných, dostaneme rovnicu pre hľadanú rýchlosť
![]() (2.3.22)
(2.3.22)
Po konkrétnom dosadení funkčnej závislosti Fx = Fx (t) do rovnice (2.3.22), vypočítame hľadanú rýchlosť, z ktorej následne určíme polohu skúmaného objektu
![]() (2.3.23)
(2.3.23)
Konštanty C1 a C2 stanovíme z konkrétnych počiatočných podmienok.
3/
Pôsobiaca sila je funkciou polohy
Fx = Fx(x)
Takýto prípad sa dá šikovnejšie riešiť ak využijeme súvislosť práce so zmenou kinetickej energie, pri zadaných počiatočných podmienkach x0 a v0 . Pre prácu pôsobiacej sily platí
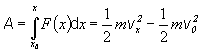 (2.3.24)
(2.3.24)
Ak primitívnou funkciou k funkcii Fx(x)je funkcia f(x), pre kvadrát hľadanej rýchlosti dostaneme
![]()
![]()
Po separácii premenných dostaneme diferenciálnu rovnicu
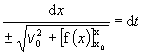 (2.3.25)
(2.3.25)
Po integrácii danej rovnice určíme hľadanú závislosť x = x(t).
4/ Pôsobiaca sila je funkciou rýchlosti Fx = Fx(vx)
Newtonovu pohybovú rovnicu (2.3.20) napíšeme v tvare
![]()
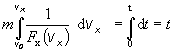 (2.3.26)
(2.3.26)
Po integrovaní rovnice (2.3.26) na ľavej strane získame funkciu f(vx), z ktorej si vyjadríme hľadanú funkčnú závislosť pre rýchlosť vx . Z nej následne po integrácii, určíme hľadanú polohu
![]() (2.3.27)
(2.3.27)
Riešenie pre konkrétny prípad sily demonštruje nasledujúci príklad.
Príklad 2.3.3: Nájdite časovú
závislosť dráhy pádu guličky s objemom V
v reálnej kvapaline s hustotou r,
ktorá má koeficient viskozity h,
ak guličku považujeme za hmotný bod. (Sila odporu prostredia je priamoúmerná
rýchlosti guličky v kvapaline F0
= 6 p h r v )
Riešenie: Zvoĺme
si súradnicovú sústavu s osou y
orientovanou zvisle nadol. Na guličku pôsobia sily: tiažová sila zvisle nadol, na základe Archimedovho zákona pôsobí vztlaková sila zvisle nahor a ak
uvažujeme reálnu kvapalinu, pôsobí ešte sila
odporu prostredia proti pohybu, t.j. zvisle nahor. Pohybovú rovnicu, nakoľko a = [0,a,0] , v
= [0,v,0] , g
= [0,-g,0] možno napísať
Ma = mg - r g V - 6 p h r v (1)
![]() (2)
(2)
Prvý
člen na pravej strane rovnice (2) je
konštanta, rovnako ako i koeficient pri druhom člene s rýchlosťou v. Pre zjednodušenie zápisu si zavedieme konštanty :
![]() (3)
(3)
![]() (4)
(4)
Rovnica
(2) prejde, po nahradení konštantami (3) a (4) a po separácii premenných, na tvar
![]() (5)
(5)
Po
integrovaní dostaneme integrál, ktorý riešime substitúciou A – B v = z ![]() dv = - dz/B
dv = - dz/B
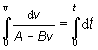
![]()
![]()
![]()
![]() (6)
(6)
![]() (7)
(7)
Rýchlosť
guličky bude narastať z nulovej hodnoty na začiatku merania na konštantnú hodnotu vr, do okamihu, kedy sa sila smerujúca nahor vyrovná so
silou tiažovou. Po tomto okamihu sa bude pohybovať rovnomerným pohybom
s konštantnou rýchlosťou, pre ktorú
platí
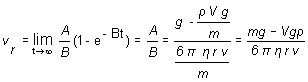
Polohu
guličky určíme riešením diferenciálnej rovnice (6), po dosadení za
rýchlosť
![]()
![]()
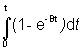
![]()
________________________________________
Príklad 2.3.4: Teleso
o hmotnosti m sa dalo z pokoja do priamočiareho
pohybu pod účinkom tiažovej sily.
Nájdite závislosť zrýchlenia, rýchlosti a dráhy pohybu hmotného bodu od času, ak odpor prostredia nezanedbáme a sila
odporu je priamoúmerná rýchlosti hmotného bodu.
Riešenie: Pohybový
stav telesa určuje výslednica pôsobiacich síl. V našom prípade sa jedná o tiažovú silu FG = mg
a silu odporu vzduchu Fo = -b v , kde b je konštanta. Výsledná sila Fv
= FG + Fo je funkciou len rýchlosti v telesa.
V karteziánskej súradnicovej sústave si vyjadríme pôsobiace sily: FG
= [0,
0, -mg ] Fo
= [0,
0, bv ] Fv = [0, 0, -mg + bv ]. Výsledný pohyb sa bude konať po
priamke rovnobežnej so z- osou
v smere nadol. Z tohto dôvodu vektorová rovnica prejde na jednu skalárnu rovnicu :
Fz = ma
, (1)
pretože
a = [0, 0, a]. Určiť zákon
pohybu telesa, t.j. časovú závislosť rýchlosti
v = v(t) a polohového vektora r = r(t), znamená riešiť rovnicu
-mg
+ bv = ma (2)
![]()
s počiatočnými podmienkami vo
= v(t =o) = 0. Po dosadení za
zrýchlenie
![]()
dostaneme separovateľnú
diferenciálnu rovnicu prvého rádu. Po separácii premenných
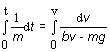 (3)
(3)
a integrácii pomocou substitúcie dostaneme
![]()
![]()
![]()
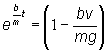
odkiaľ pre hľadanú rýchlosť platí:
![]() (4)
(4)
Veľkosť zrýchlenia ako
funkciu času získame po zderivovaní rýchlosti, t.j. vzťahu určeného rovnicou
(4)
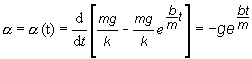
resp. vo vektorovom tvare
![]() (5)
(5)
Časovú závislosť polohy získame
z rovnice (4) po dosadení za rýchlosť
![]()
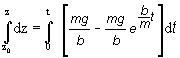
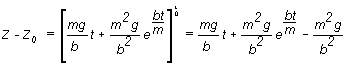
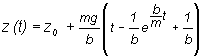
r
= r(t) = z(t) k
Príklad 2.3.5 Experimentálne
merania na objekte s hmotnosťou
500 g ukázali, že pri pohybe v rovine
x y sa jeho pohyb mení podľa rovníc : x = t
-A t2, y = B t3,
kde t je čas v sekundách, x, y sú súradnice v metroch, A = 4 m.s-2 a B =
0,1 m.s-3 sú konštanty. Nájdite: a) vzťah pre pôsobiacu silu, b) veľkosť pôsobiacej sily
v okamihu t1 = 10 s.
Riešenie: Zadané
veličiny: m = 500 g = 0,5 kg , t1 = 10 s
parametrické
rovnice dráhy: : x = t -A t2,
y = B t3 , A
= 4 m.s-2 a B = 0,1 m.s-3
Pôsobiacu
silu určíme na základe 2. Newtonovho zákona v zložkovom tvare:
![]()
![]()
![]()
![]()
a)
F = Fx i + Fyj = 2m( -Ai + 3Btj)
b) F
= F(t) = 2 m ![]()
![]()
_________________________
Príklad 2.3.6:
Nájdite vzťah určujúci časovú závislosť rýchlosti telesa pohybujúceho sa vo vzduchu s hustotou r
, ak aerodynamický koeficient odporu pohybujúceho sa telesa je k a
jeho čelný prierez je S, ak viete, že sila odporu vzduchu je daná vzťahom
![]()
Riešenie:
Na dané teleso pôsobí sila tiaže v smere pohybu a sila trenia, ktorá
smeruje proti smeru pohybu. Ak si
zvolíme kladnú os v smere pohybu, pre tento pohyb po priamke v smere
osi y platí:
![]() (1)
(1)
Po úprave separovateľnej diferenciálnej
rovnici (1) prvého rádu dostaneme
dv = g( 1 - A2 v2)dt
kde sme zaviedli konštantu
![]() .
.
Po
separácii premenných a integrovaní získame rovnicu
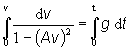 (2)
(2)
Integrál na ľavej strane rovnice (2) riešime
rozkladom na parciálne zlomky.
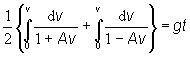
![]()
![]()
![]()
1- Av = ( 1+Av )
e -2Agt
1 - e-2Agt
= Av ( 1 + e-2Agt)
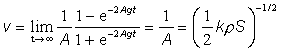
Vidíme, že pri voľnom páde v prostredí, ktorého odpor nezanedbávame, rýchlosť sa ustáli na hodnote, ktorá závisí od tvaru a veľkosti telesa a od vlastností prostredia, v ktorom sa pohyb uskutočňuje.
Kontrolné otázky k časti 2.3.5
1. Napíšte základnú pohybovú rovnicu hmotného bodu.
2. Na konkrétnych príkladoch uveďte, kedy sa stretávame s počiatočnými podmienkami.
3. Vysvetlite, čo znamená riešiť pohybovú rovnicu.
4. S ktorými prípadmi pôsobiacej sily sa možno najčastejšie stretnúť? Ako budeme pre tieto prípady riešiť pohybovú rovnicu?
5. Ako možno využiť princíp superpozície pri riešení pohybovej rovnice hmotného bodu?