2.3.7 Sily v neinerciálnych sústavách
Skúmajme pohyb častice (resp. hmotného bodu), na ktorý pôsobí sila F. Ak skúmame pohyb častice z hľadiska absolútnej sústavy S, pre časticu platí Newtonova pohybová rovnica F = ma. Chceme vedieť ako sa zmení pohybová rovnica tej istej častici, pohybujúcej sa za rovnakých podmienok, ale vzhľadom na neinerciálnu sústavu S´. Prv než pristúpime k matematickému riešeniu tohto problému, ozrejmime si ho na nasledujúcom experimente:
Predstavme si, že sme si urobili výlet do sveta našej slnečnej sústavy. Nasadli sme na raketoplán a naša Zem je už len maličkou hviezdičkou. Sme ďaleko od príťažlivých telies. Čo sa deje s našimi vecami v raketopláne, ak máme motor vypnutý? Teplomer je v divnej polohe, tak isto kyvadlo hodín sa zastavilo v akejsi polohe, rôznej od zvislého smeru. Predmety i naše meracie prístroje sa vznášajú v kabíne. Vysvetliť túto skutočnosť vieme, nenachádzame sa na Zemi, ale v medziplanetárnom priestore, v ktorom predmety stratili tiaž. Čo sa stane, ak sa rozhodneme zapnúť motor raketoplánu a začne sa pohybovať rovnomerne zrýchleným pohybom? Predmety, ktoré sa vznášali okolo nás sa dali do pohybu. Akým smerom a akou rýchlosťou? Ak raketoplán sa pohybuje so zrýchlením 9,81 m.s-2 cítime sa ako doma. Teplomer „spadol“, hodiny sa dali do vertikálnej polohy. Ak pustíme tenisovú loptičku a zmeriame, s akým zrýchlením padá, dospejeme k výsledku, že zrýchlený pohyb loptičky bude čo do veľkosti vždy taký, ako zrýchlenie nášho raketoplánu. Smer „padania“ loptičky bude vždy opačný ako smer pohybu raketoplánu. To platí pre všetky predmety vo vnútri lode. Ak sa pohybuje raketoplán dopredu, všetky predmety sa pohybujú smerom opačným - dozadu. Toto pozorovanie možno sformulovať nasledovne: Ak sa raketoplán pohybuje s určitým zrýchlením, telesá v ňom začínajú mať „tiaž“. Pritom „príťažlivá sila“ má smer opačný ako vektor zrýchlenia raketoplánu a zrýchlenie voľného „pádu“ telies sa veľkosťou rovná zrýchleniu raketoplánu. Zaujímavosťou je, že pozorovaním nemôžeme odlíšiť zrýchlený pohyb systému od príslušnej príťažlivej sily. To znamená, že ak okná v raketopláne máme zakryté, nerozlíšime, či je raketoplán v pokoji, alebo sa pohybuje so zrýchlením 9,81 m.s-2. Rozdiel však je v smeroch pôsobiacich zrýchlení. Na Zemi smeruje príťažlivá sila do stredu Zeme. To znamená, že smery zrýchlenia v dvoch rôznych bodoch na Zemi tvoria medzi sebou uhol. V raketopláne, ktorý sa pohybuje zrýchlene, sú smery príťažlivosti vo všetkých bodoch presne paralelné. Na Zemi sa mení zrýchlenie s výškou, v raketopláne so zrýchleným pohybom tento efekt nevzniká. Napriek týmto odlišnostiam možno považovať zrýchlenie a pôsobenie príťažlivej sily za ekvivalentné.
Takmer úplná rovnocennosť zrýchlenia
a pôsobenia príťažlivej sily nazývame princíp ekvivalencie. Tento princíp umožňuje riešiť mnohé úlohy
pomocou fiktívnej príťažlivej sily, ktorá sa javí v systémoch pohybujúcich
sa zrýchlene. Uvidíme, že pohybovú rovnicu v neinerciálnom systéme je
možné riešiť obdobne ako
v inerciálnom systéme, ak k výslednici síl pôsobiacich na teleso
pridáme sily fiktívne, súvisiace
s neinerciálnosťou systému, ktoré nazveme spoločným názvom silami
zotrvačnými.
Z nášho medziplanetárneho výletu sa vráťme ku kinematike a k
rovniciam pre rýchlosť zloženého
pohybu a k zrýchleniu
zloženého pohybu. Ukážeme si, ako súvisia tieto rovnice s výsledkami nášho experimentu.
Pri skúmaní zloženého pohybu sme si odvodili vzťah (2.1.132) pre zrýchlenie častice pohybujúcej sa v neinerciálnej sústave
a´ = a - a 0 - 2 (w ´ v´) - w ´ (w ´ r´) - a ´ r´
v ktorej a0 určuje zrýchlenie začiatku pohybujúcej sa sústavy S´, t.j. bodu O´ vzhľadom na začiatok pevnej sústavy, t.j. bod O ; w a a sú uhlová rýchlosť a uhlové zrýchlenie sústavy S´ voči sústave S , v´ a r´ je vektor rýchlosti a polohový vektor hmotného bodu v sústave S´. Ak vynásobíme túto rovnicu hmotnosťou uvažovanej častice dostaneme rovnicu
m a´ = m a - m a0 - 2 m (w ´ v´) - m w ´ (w ´ r´) - m a ´ r´ (2.3.35)
udávajúcu pohybovú rovnicu hmotného bodu v neinerciálnej sústave F´ = ma´. F´ predstavuje výslednicu všetkých síl pôsobiacich na hmotný bod v sústave S´. Je určená vektorovým súčtom
F´ = F + F0 + Fc + Fod + FE (2.3.36)
ktorých význam je nasledovný:
·
F je vonkajšia sila pôsobiaca na hmotný bod, majúca pôvod vo vzájomnom
pôsobení materiálnych objektov na hmotný bod, preto sa niekedy tejto sile hovorí
sila pravá, resp.
sila skutočná.
·
F0
= - m a0 je tzv. postupná
zotrvačná sila, vznikajúca v dôsledku zrýchleného pohybu začiatku
sústavy S´. Pozorovateľovi vo vnútri
neinerciálnej sústavy sa javí, že táto sila sa snaží zrýchľovať tento hmotný
bod vzhľadom k tejto sústave.
·
FC
= - 2 m(w
´ v´)
je tzv. Coriolisova sila,
ktorá pôsobí na telesá pohybujúce sa v neinerciálnej sústave
rýchlosťou v ´ rôznobežnou
s osou otáčania. Jej veľkosť
závisí od orientácie vektorov w a v
´ .
·
Fod = - m w ´ (w
´ r´)
je tzv. zotrvačná odstredivá
sila. Táto sila má pôvod v rotačnom pohybe sústavy. Často sa stretávame s jej názvom ako radiálna príťažlivá sila. (Pozn.: Pri
rovnomernom pohybe po kružnici časť 2.1.4 sme sa stretli už s pojmom
odstredivá sila. Jedná sa o rôzne sily).
· FE = - (a x r¢ ) je tzv. Eulerova sila, ktorá je od nuly rôzny vtedy, keď uhlová rýchlosť otáčania nie je konštantná, ale sa mení s časom.
Sily, F0 , Fc , Fod a FE nazývame spoločným názvom zotrvačné sily. Všetky štyri zotrvačné sily sa javia pozorovateľovi v pohybujúcej sa neinerciálnej sústave ako sily poľa, pretože nie sú spôsobené dotykom iných telies. Zatiaľ čo sily F0 , FE , Fod existujú nezávisle na pohybe hmotného bodu vzhľadom na neinerciálnu súradnicovú sústavu S´, Coriolisova sila Fc existuje len ak smer vektora rýchlosti nie je kolineárny (rovnobežný) so smerom vektora uhlovej rýchlosti a mení sa so sínusom uhla ich vzájomnej orientácie.
U zotrvačných síl nie je možné určiť konkrétne teleso, ktorého pôsobením tieto sily vznikajú. Preto zotrvačné sily nemajú sily reakcie. E. Mach vyslovil predpoklad, že zotrvačné sily vznikajú vo vzťažných sústavách pohybujúcich sa so zrýchlením ( postupným i rotačným) vzhľadom na vzdialené nebeské hviezdy vesmíru. Táto myšlienka zohrala svoju úlohu pri vzniku všeobecnej teórie relativity. Zotrvačné sily môžu spôsobovať zrýchlenie, konať prácu, je ich možné skladať s inými silami. (Pozn.: Preto nie je najvhodnejšie používať názov „fiktívne sily“, s ktorým sa v niektorých prípadoch stretávame.) Zo vzťahu pre zotrvačné sily plynie, že zrýchlenia, ktoré udeľujú telesám ( hmotným bodom), nie sú závislé na ich hmotnosti. Táto vlastnosť ich odlišuje od síl „skutočných“, ktoré majú pôvod vo vzájomnom pôsobení materiálnych telies. Skutočné resp. pravé sily, udeľujú telesu zrýchlenie, ktoré je nepriamo úmerné ich hmotnosti (a =F/m).
V neinerciálnych sústavách Newtonov zákon sily neplatí. To znamená, že pohybové rovnice, platné pre inerciálne sústavy, riešiť v neinerciálnej sústave bez istej úpravy nie je možné. Akú úpravu je nutné urobiť? Náš medziplanetárny experiment a štruktúra matematického vyjadrenia pohybovej rovnice v neinerciálnej sústave (2.3.35), ktorá má zhodnú štruktúru „súčin hmotnosti a zrýchlenia sa rovná sile“ ukázujú, že ak Newtonovu pohybovú rovnicu chceme použiť v neinerciálnej sústave, ku skutočným silám pôsobiacim na hmotný bod od okolitých materiálnych objektov musíme ešte pripočítať príslušné zotrvačné sily.
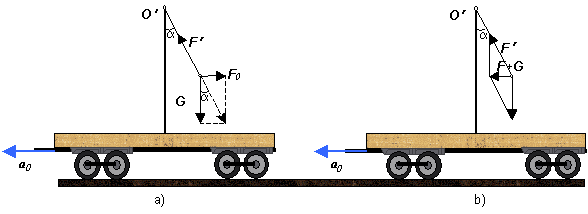
Ilustráciu riešenia pohybu v inerciálnej a v neinerciálnej vzťažnej
sústave urobíme na príklade hmotného bodu zaveseného na vlákne zanedbateľnej
hmotnosti, ak bod závesu vlákna O´ je
pevný v sústave, ktorá sa pohybuje vzhľadom k inerciálnej vzťažnej
sústave s translačným zrýchlením a0.
__________________________________________________________________________
Príklad 2.3.7: Nájdite
podmienku rovnovážneho stavu
matematického kyvadla zaveseného v pohybujúcom sa vagóne so
zrýchlením a0 vzhľadom k Zemi z hľadiska neinerciálnej vzťažnej sústavy (vagón) a z hľadiska
vzťažnej sústavy, ktorú možno považovať za inerciálnu sústavu (Zem).
Riešenie: Matematické kyvadlo je hmotný bod zavesený na nehmotnej
niti. Uvažujme sily, ktoré pôsobia na hmotný bod a) v neinerciálnej vzťažnej sústave:
· sila F´, ktorá pôsobí na hmotný bod zo
strany závesu,
· tiaž hmotného bodu G
· sila zotrvačnosti F0. (Pozn.: Jedinou
nenulovou zotrvačnou silou v prípade translačného pohybu je postupná
zotrvačná sila F0.)
Pohybová rovnica hmotného bodu v neinerciálnej sústave,
t.j. v sústave pevne spojenej s vagónom je
ma´ = F´+ G + F0
pričom
stav rovnováhy odpovedá podmienke
0 = F´+ G + (- m a´
)
Pre
uhol a medzi dvomi
polohami kyvadla - v kľude a pri
pohybe so zrýchlením a0, platí
tg a = ![]()
b) v inerciálnej
vzťažnej sústave (obr. b) sú to sily:
·
tiaž G
·
sila F´
Pohybová
rovnica hmotného bodu v inerciálnej sústave, t.j. v sústave pevne
spojenej so Zemou je
ma = F´+ G
a podmienka rovnováhy je
ma = F´+ G = m a0
Pre polohu
závesu platí
tg a = 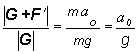
Vidíme, že obidva postupy vedú k rovnakému výsledku.( Pozn.: Musíme
mať však na zreteli, že pri riešení problému sme pristupovali osobitne
z hľadiska neinerciálneho a osobitne z hľadiska inerciálneho. Nikdy
nemôžeme kombinovať opis súčasne z hľadisku neinerciálneho i
z hľadiska inerciálneho.)
___________________________________________________________________________
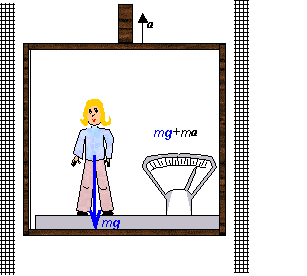
Príklad 2.3.8: Dievča s hmotnosťou m stojí na váhach, ktoré sú umiestnené v kabíne výťahu. Rozhodnite,
či váhy ukážu rovnakú výchylku, ak výťah
a) je v kľude, b) rozbieha
sa so zrýchlením a smerom nahor c) pohybuje sa so spomalením a smerom nahor, d) pohybuje sa so
zrýchlením a smerom nadol, e) so spomalením a smerom nadol. Kedy bude dievča
relatívne najspokojnešie so svojou hmotnosťou, ak dbá o svoju štíhlu
líniu?
Riešenie:
a) Výťah v pokoji predstavuje inerciálny systém, v ktorom
jedinou pôsobiacou silou je tiažová sila . Ak si zvolíme súradnicovú sústavu
s osou z orientovanou smerom nadol, pôsobiaca tiaž v tejto
sústave je určená G = (0,0,G) . Váhy v pokoji
ukážu výchylku, odpovedajúcu tiaži dievčaťa G = mg.
b) Ak sa výťah pohybuje so zrýchlením a , jedná sa o neinerciálny vzťažný
systém. Ak v ňom cheme uplatniť Newtonovu pohybovú rovnicu musíme
k skutočnej tiažovej sile pripočítať sily zotrvačné. Počas pohybu výťahu so zrýchlením a vzniká dodatočná príťažlivá sila smerom opačným ako zrýchlenie, ktoré ju vyvolalo.
Pohybová rovnica vo vektorovom tvare pre neinerciálny systém bude
ma = G + F0
Sila zotrvačnosti (dodatočná príťažlivá sila) a zemská príťažlivosť
majú smer v jednej priamke. V prípade pohybu výťahu so zrýchlením a smerom nahor, bude zotrvačná
sila F0 = (0,0, ma ). Vektorová pohybová rovnica
prejde na skalárny tvar
m a = mg + ma = m(g + a)
Váha ukáže väčšiu
výchylku, zväčšenú práve o súčin
ma .
b) V prípade pohybu so spomalením a smerom nahor, vektor zrýchlenia
neinerciálnej sústavy má smer nadol, takže dodatočná príťažlivá sila
zotrvačnosti má smer opačný, t.j. smerom
nahor
F0 = (0,0, - ma ), takže pohybová rovnica prejde
na tvar
m a = mg - m a = m( g - a)
Váha ukáže menšiu výchylku práve o súčin ma vzhľadom na výchylku váh v stave, keď výťah je
v kľude.,
d) V prípade keď výťah sa pohybuje so zrýchlením a smerom nadol, dodatočná
príťažlivá sila zotrvačnosti má smer
opačný t.j. F0 = (0,0, - m a) a pohybová rovnica bude
m a = m a - m a = m( g - a)
Váha ukáže opäť
menšiu výchylku práve o súčin m
a.
e) V prípade pohybu výťahu
so spomalením a smerom nadol, vektor zrýchlenia neinerciálnej sústavy má
smer nahor, takže dodatočná príťažlivá
sila zotrvačnosti má smer opačný, t.j. smerom nadol F0 = (0,0, m a). Pohybová rovnica má tvar
m a = mg + ma = m( g + a)
Váha ukáže väčšiu výchylku odpovedajúcu práve súčinu m a.
e) V prípade pohybu výťahu
so spomalením a smerom nadol vektor zrýchlenia neinerciálnej sústavy má smer nahor, takže dodatočná príťažlivá sila
zotrvačnosti má smer nadol F0 = (0,0, ma) a pohybová rovnica má tvar
m a = mg + m a = m( g + a)
Váhy ukážu väčšiu výchylku práve o súčin m a.
Dievča, ktoré dbá o svoju štíhlu líniu, bude „ relatívne“
najspokojnejšie so svojou hmotnosťou m, ak sa bude vážiť buď
v brzdiacom výťahu smerom nahor resp. v rozbiehajúcom sa výťahu
smerom nadol. V obidvoch prípadoch váhy
ukážu menšiu hodnotu, ktorá od
skutočnej tiaže mg sa
zmenší o dodatočnú tiaž m a. V týchto prípadoch
všetky telesá, ktoré sú vo
výťahu, akoby boli ľahšie. Čím väčšie je zrýchlenie výťahu, tým väčšia je
strata tiaži.
__________________________________
Príklad 2.3.9 Fyzikálne vysvetlite pozorované
zmeny pohybového stavu chlapca
stojaceho v autobuse, ktorý sa rozbieha so zrýchlením resp.,
ktorý brzdí. Svoje úvahy
graficky znázornite.
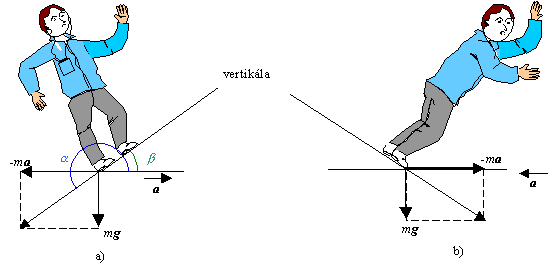
Riešenie: Zrýchlene pohybujúci sa autobus je neinerciálny vzťažný systém. Ak
chceme riešiť pohybovú rovnicu musíme ku skutočnej tiažovej sile zvážiť i sily
zotrvačné. Jedinou zotrvačnou silou je,
opäť ako v prípade výťahu, postupná zotrvačná sila, ktorá má však
smer kolmý na zemskú príťažlivosť. To vyvoláva zvláštne pocity u každého cestujúceho. Ak autobus sa rozbieha
so zrýchlením a (obr. a), vzniká dodatočná sila, ktorá má opačný smer ako
zrýchlený pohyb autobusu. Zložíme túto silu s príťažlivou silou
Zeme. Na chlapca, ktorý je v autobuse, bude pôsobiť sila, ktorá so smerom
pohybu zviera tupý uhol (a ) . Keď chlapec stojí tvárou v smere pohybu, cíti, že sa autobus
pohol. Aby nespadol, musí sa postaviť „vertikálne“. Okamžitá vertikála bude
šikmá. Chlapcova vertikála zviera ostrý
uhol (![]() ) so smerom pohybu.
Ak chlapec bude stáť a nebude sa niečoho držať, určite spadne dozadu. Ak autobus brzdí (obr. b),
chlapcova vertikála sa nakláňa dozadu. Chlapcovi v okamžiku začiatku
brzdenia sa zdá, že ho niekto strčil do
chrbta (vertikálu má za chrbtom).
V takejto polohe však nezostáva nadlho. Autobus zastavuje, spomalenie sa
stráca a „vertikála“ prechádza do pôvodného stavu. Treba opäť meniť polohu
tela. Chlapec sa narovná. Má pocit
akoby ho niekto strčil do hrude.
) so smerom pohybu.
Ak chlapec bude stáť a nebude sa niečoho držať, určite spadne dozadu. Ak autobus brzdí (obr. b),
chlapcova vertikála sa nakláňa dozadu. Chlapcovi v okamžiku začiatku
brzdenia sa zdá, že ho niekto strčil do
chrbta (vertikálu má za chrbtom).
V takejto polohe však nezostáva nadlho. Autobus zastavuje, spomalenie sa
stráca a „vertikála“ prechádza do pôvodného stavu. Treba opäť meniť polohu
tela. Chlapec sa narovná. Má pocit
akoby ho niekto strčil do hrude.
Zotrvačné sily spôsobené rotačným pohybom
Nakoľko naša Zem je neinerciálna sústava ozrejmime si viaceré skutočnosti, ktoré súvisia so zotrvačnými silami, s ktorými sa stretávame v praktickom živote. Pohyb rotačného systému sa určuje počtom otáčok za jednotku času, ktoré systém vykoná okolo svojej osi. Treba prirodzene poznať aj smer rotácie.
1/
Sila odstredivá
Aby sme si zvláštnosti spôsobené rotačným pohybom ozrejmili uvažujme najprv „koleso smiechu“, ktoré je mám dobre známe z lunaparkov. Je to v podstate hladký disk s priemerom niekoľko metrov, ktorý sa otáča. Možno sa na tomto kolese udržať? Aj tí, ktorí sa nezamýšľajú nad fyzikou, zo skúsenosti vedia, že sa majú postaviť do stredu disku, pretože čím ďalej od stredu disku sú, tým je ťažšie sa na ňom udržať. Vysvetlime si túto skutočnosť.
Disk predstavuje neinerciálny systém. Každý predmet spojený s diskom sa pohybuje po kružnici s polomerom R so zrýchlením v2/R. Z hľadiska neinerciálneho pozorovateľa to znamená vznik dodatočnej sily mv2/R, ktorá smeruje pozdĺž polomeru od stredu. Táto sila pôsobí v ľubovolnom bode disku. Pre body, ktoré ležia na tej istej kružnici, bude veľkosť zrýchlenia rovnaká. Určime si jej závislosť od vzdialenosti od stredu.
Označme si počet otáčok, ktoré urobí disk za sekundu f. Dráha, ktorú prejde bod nachádzajúci sa na disku v mieste určenom s polomerom kružnice R za čas t je s = 2pRf = vt.. Dráha, ktorú prejde tento bod za 1 s je vlastne určená jeho rýchlosťou v = 2pRf. Pre zrýchlenie po dosadení za rýchlosť dostávame
![]()
a = 4p2f2R (2.3.37)
Zrýchlenie sily, pôsobiacej na otáčajúcom sa disku vzrastá priamo úmerne so vzdialenosťou od stredu kolesa . To znamená, že na rôznych kružniciach bude zotrvačná sila rôzna a teda aj smery „vertikál“ pre telesá v rôznych vzdialenostiach od stredu disku budú rôzne. Vyplýva to z vektorového súčtu pôsobiacich síl. Výsledná sila je určená ako uhlopriečka v obdĺžniku, dvoch navzájom kolmých síl - tiažovej sily, v dôsledku zemskej príťažlivosti a sily zotrvačnosti, v dôsledku neinerciálnosti systému. Príťažlivá sila Zeme má vždy rovnakú veľkosť pre všetky body kolesa. Sila zotrvačnosti sa zväčšuje so vzdialenosťou od stredu kolesa a teda výslednica síl sa bude odkláňať tým viac od smeru zemskej vertikály, čím ďalej je bod od stredu disku vzdialený.
Človek nachádzajúci sa na kolese smiechu sa tým viac nakláňa, čím je vzdialenejší od stredu kolesa a pri istých rýchlostiach a polomere nie je schopný už sa na ňom udržať.
Možno si opäť položiť otázku. Je možné vymyslieť taký systém, aby sa človek na tomto otáčajúcom systéme udržal? Prirodzene, je to možné, ale disk by sme museli zameniť za taký, ktorý by mal povrch prispôsobený tak, že výsledná príťažlivá zotrvačná sila by bola všade kolmá na povrch. Na základe výpočtov, tvar takéhoto povrchu bude paraboloid. (Vzniká otáčaním paraboly okolo svojej osi. Každý vertikálny prierez touto plochou je parabola.) Takúto plochu možno napríklad vytvoriť, ak rýchlo roztočíme nádobu s vodou.
Jav odstredivosti sa veľmi využíva v technike. Na použití tohto javu
je založená odstredivka. Je to nádoba
(bubon), ktorá sa rýchlo otáča okolo svojej osi. Nech priemer odstredivky je dostatočne veľký a odstredivku naplnenú
vodou roztočíme. Vhodíme do nej raz kovovú guličku a neskôr korkovú zátku.. Pozorujeme rozdiel v chovaní sa
týchto dvoch predmetov? Prv než
budeme zvažovať chovanie sa v otáčajúcom sa systéme, zvážme ako sa budú
tieto dva predmety chovať v nádobe naplnenou vodou v kľude. Kovová
gulička sa nám ponorí, kým korková zátka pláva. Pri roztočenom bubne už vieme,
že vzniká dodatočná odstredivá
zotrvačná sila, ktorej zrýchlenie so vzdialenosťou od jej stredu
priamoúmerne vzrastá. Na základe existencie tejto sily, kovová gulička bude klesať ku dnu, nie však po našej
vertikále. Ustavične sa bude vzďaľovať od osi otáčania a bude sa posúvať smerom k stene bubna, na ktorom sa
až zastaví. Korková zátka sa bude, naopak, pohybovať v smere k osi
otáčania a tam sa umiestni. Na tomto princípe pracujú odstredivky na čistenie
kalnej vody, respektívne, zariadenia na oddeľovanie pevných alebo kvapalných
prímesí, ktoré nazývame separátory.
Ak je hmotný bod v pokoji a sústava koná len rotačný pohyb s konštantnou uhlovou rýchlosťou (a0 = 0, a = 0) na hmotný bod vzhľadom na neinerciálnu sústavu pôsobí len zotrvačná odstredivá sila
Fod = mw´(w´ r´) = m r´^w2
kde r´^ je kolmá vzdialenosť hmotného bodu od osi otáčania. Častá chyba v pochopení odstredivej sily vychádza z toho, že pojem „odstredivá sila“ sa inokedy používa v inom zmysle. Za odstredivú silu je považovaná sila reakcie, ktorou hmotný bod A rotujúci po kružnici, pôsobiaci na hmotný bod B nútiaci ho, prostredníctvom väzby (vlákna), vykonávať rotačný pohyb. Rovnako veľká a opačne orientovaná sila, ktorou hmotný bod B pôsobí na rotujúci hmotný bod A, je sila dostredivá, Tieto sily sú však silami pôsobiacimi na dve rôzne telesá. Sú to skutočné (reálne) sily v zmysle newtonovskej mechaniky, ako výsledok vzájomného pôsobenia materiálnych objektov.
Pokiaľ
budeme hovoriť o odstredivej sile, nebudeme ju chápať v tomto zmysle, ale
ako zotrvačnú silu existujúcu len v rotujúcej vzťažnej sústave, ktorá však zanikne, ak sústava prejde do
inerciálnej vzťažnej sústavy. Niektoré príklady odstredivých síl a jej
technické využitie sme si už uviedli v prebraných príkladoch. Záverom
možno zhrnúť:
· Odstredivá sila sa vyskytuje pri rotačnom pohybe zotrvačníkov, rotorov, elektromotorov a turbín.
· Odstredivá sila pôsobí na osoby i telesá vo vozidlách, konajúcich krivočiary pohyb.
· Odstredivá sila vyvoláva preťaženie pôsobiace na pilotov (cestujúcich) pri krivočiarom pohybe lietadla.
· Odstredivá sila pôsobí na rotujúce nebeské telesá ( umelé družice, planéty).
· Odstredivá sila zmenšuje príťažlivú gravitačnú silu
_____________________________________________________________________
Príklad 2.3.10: Rozhodnite, či tiaž telesa na póle a na rovníku je rovnaká. Svoje
tvrdenie fyzikálne zdôvodnite. Určite o koľko je ľahšie kilogramové závažie na
rovníku ako na póle za predpokladu, že
Zem má presne tvar gule o polomere R.
Riešenie: Telesá nachádzajúce sa na rôznych miestach zemského povrchu sa
nachádzajú v rôznych vzdialenostiach od osi Zeme, čo závisí od jeho
zemepisnej šírky. Pri prechode od pólu k rovníku sa táto vzdialenosť
zväčšuje. Odstredivá sila je určená
aod = - w ´
(w ´ r´)
Ak si vyjadríme uhlovú rýchlosť otáčania Zeme w pomocou počtu otáčok za
jednotku času f, pre veľkosť odstredivého zrýchlenia platí vzťah
aod
= 4 p2 f2 r´
Teleso na póle je na osi otáčania,
takže r´ = 0 a odstredivé zrýchlenie je rovné nule. Na póle zotrvačná
odstredivá sila nepôsobí. Tiaž telesa na póle je určená len silou mg.
Odstredivá zotrvačná sila sa pri prechode od pólu k rovníku zväčšuje,
pretože sa zväčšuje vzdialenosť telesa od osi rotácie. Na rovníku je odstredivá
sila maximálna. Odstredivá sila má smer pozdĺž polohového vektora r´ . Označme si Gr tiaž, ktorú
nameriame na rovníku.
Gr = mgr = m (g - aod) = m (g - 4 p2 f2 R)
Zmena tiaže na rovníku bude pre teleso o hmotnosti m
D G = G - Gr = m 4 p2 f2 R
Po číselnom vyjadrení dostaneme pre zmenu tiaže kilogramového závažia
D G = 1 kg. 4. 3,142.
(1/86 400 s)2. 6 378 000 m = 0,033778 N
![]()
Pozn. V skutočnosti
stráca kilogramové závažie ešte viac, pretože Zem je elipsoid (sploštená guľa).
Vzdialenosť od pólu do stredu Zeme je menšia ako polomer Zeme na rovníku,
priemerne o 1/300 jeho veľkosti.
![]()
Kontrolné otázky k časti 2.3.7
1. Vysvetlite pojem sily fiktívne resp. zotrvačné a uveďte ich príklad.
2. Zapíšte rovnicou Coriolisovú silu a vysvetlite jej význam.
3. Kedy vzniká Coriolisová sila? Uveďte konkrétne príklady.
4. Napíšte matematicky zotrvačnú odstredivú silu. V ktorých systémoch sa s ňou stretávame?
5. Čo rozumieme pod pojmom „zotrvačné sily“?
6. Pri pohybe výťahu máme niekedy zvláštne pocity v žalúdku. Viete vysvetliť ich príčinu?
7. Prečo strácame rovnováhu, ak stojíme v rozbiehajúcom sa, alebo brzdiacom autobuse?
8. Akým smerom sa budeme pohybovať, v prípade, že sa nedržíme pri jazde autobusom a autobus prudko začne brzdiť?
9. Ak rieka tečie v smere zemského poludníka, vymývajú sa obidva brehy rovnako? Svoju odpoveď fyzikálne zdôvodnite.
10. Ako vysvetlíte vírivý pohyb vody pri jej vypúšťaní z umývadla?
11. Vyteká voda z umývadla rovnako na severnej a južnej pologuli? Svoju odpoveď zdôvodnite.