4.1.9. 2  Tepelná vodivosť

Ak plyn v rôznych miestach nádoby má rôznu teplotu, a teda aj rôznu strednú kinetickú energiu častíc, potom vzájomnými zrážkami sa po čase tieto rozdiely vyrovnajú a plyn bude mať v celej nádobe tú istú teplotu. Prenos kinetickej energie častíc, ktorý vedie k vyrovnaniu teplôt je základom tepelnej vodivosti plynu. V tomto prípade bude b kinetická energia jednej častice E = ikT/2 a dB bude prenášané množstvo tepla dQ. Ďalej predpokladáme, že koncentrácia plynu je všade rovnaká. Potom

 

  .

 

Po dosadení do (d) v § (4.1.9)

 

  ,

 

kde K je koeficient tepelnej vodivosti plynu. Súčin

 

 

prepíšeme do inej podoby. Vieme, že molárna tepelná kapacita pri konštantnom objeme je

 

  .

 

 Z tohoto vyplýva, že ik/2 je tepelná kapacita C_V prepočítaná na jednu časticu. Keďže n je počet častíc v jednotke objemu (koncentrácia), 

 

 

 

je tepelná kapacita objemovej jednotky plynu. Hmotnosť objemovej jednotky sa číselne rovná hustote r a tepelná kapacita jednotky hmotnosti je c_V. Preto môžeme napísať

 

.

 

Potom koeficient tepelnej vodivosti

 

  .                                                                                                         (4.1.28)

__________________________

 

Príklad 4.1.9.2.1

Priestor medzi dvomi koaxiálnymi valcami s polomermi R₁ a R₂  (R₂  > R₁) je vyplnený ideálnym plynom s koeficientom tepelnej vodivosti K. Teplota vonkajšieho valca je T₂ a vnútorného T₁ , (T₁ > T₂). Nájdite tepelný tok pripadajúci na jednotku dĺžky valcov.

 

Riešenie: 

Teploty valcov sú konštantné, tok tepla bude stacionárny (nebude sa meniť s časom). Ak si predstavíme v medzere medzi valcami myslenú koaxiálnu valcovú plochu s polomerom r, bude cez ňu prechádzať rovnaké množstvo tepla ako cez každú inú takúto plochu. Na tejto myslenej ploche bude teplota T. Teplo, ktoré prejde cez plôšku dS plášťa spomenutého mysleného valca za čas dt bude podľa (a) z § 4.1.9.2 

 

  

 

a cez plochu plášťa s polomerom r a s dĺžkou l  za jednotku času prejde

 

 . 

 

Ako  sme už  spomenuli, toto  teplo nezávisí  od polomeru  mysleného plášťa, t.j. Q = const. Poslednú rovnicu upravíme tak, že rozdelíme premenné a zintegrujeme

 

 ,

 

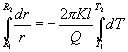 po výpočte:

 

  .

 

Odtiaľto vyjadríme Q , vydelíme ho dĺžkou l, čím dostaneme tok tepla pripadajúci na jednotku dĺžky valcov 

 

 .

____________________________