4.1. 8    Maxwellovo rozdelenie molekúl podľa rýchlostí

            V plyne v dôsledku chaotického pohybu častíc a zrážok medzi nimi sa ustáli rovnovážny stav, ktorý sa prejavuje rovnomerným rozdelením teploty a koncentrácie častíc v nádobe. Jednotlivé častice sa pohybujú rôznymi smermi a môžu mať rôzne rýchlosti v. Pravdepodobnosť toho, že častica má rýchlosť v intervale hodnôt v až (v+dv) je úmerná (pozri § 4.1.7)

 

.

 

Plyn je ideálny, jeho častice nemajú potenciálnu energiu a nepredpokladáme existenciu vonkajšieho silového poľa. Potom z celkovej mechanickej energie častice ostáva len kinetická energia. Ak je N počet všetkých častíc v objeme, potom dN je počet častíc s rýchlosťami v uvedenom intervale. Ak by sme kreslili pre jednotlivé častice (ktoré majú rýchlosť v rámci tohoto intervalu) ich vektory v z jedného bodu, tak ich konce by boli v guľovej vrstve s polomerom v a hrúbkou dv. Objem tejto vrstvy je 4pv² dv. Počet častíc s takýmito rýchlosťami je úmerný celkovému počtu častíc v objeme, hrúbke guľovej vrstvy a pravdepodobnosti výskytu rýchlostí v intervale v až v+dv

 

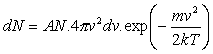  ,                                                                          (a)

 

kde A je koeficient úmernosti. Po výpočtoch  prídeme k

 

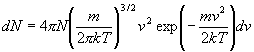                                                                 (4.1.22)                                                                 

Toto je Maxwellovo rozdelenie častíc plynu podľa rýchlostí. Vzťah nám udáva koľko častíc plynu má pri teplote plynu T rýchlosť v intervale od v do v+dv. Výraz

 

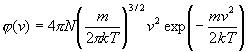                                                                    (4.1.23)

 

je Maxwellova rozdeľovacia funkcia. Keďže kinetická energia častice plynu súvisí s jej rýchlosťou, je možné rozdelenie podľa rýchlostí prepočítať na rozdelenie podľa energií (príklad 4.1.8.2).

Hodnota najpravdepodobnejšej rýchlosti   je

 

    .                                                                                                         (4.1.24)

 

Výpočet najpravdepodobnejšej energie je v príklade 4.1.8.3.

 

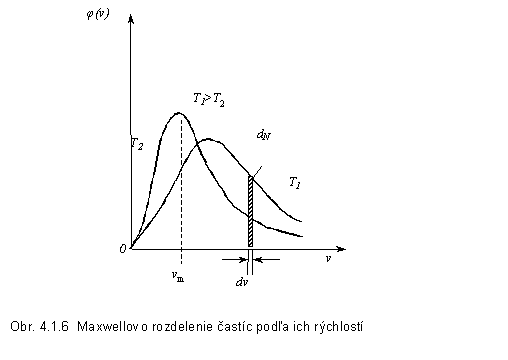
Grafické znázornenie Maxwellovej rozdeľovacej funkcie je na obr.4.1.6.  Plochy ohraničené krivkami a vodorovnou osou sú rovnaké a rovné počtu všetkých častíc N. Vo vyšrafovanom pásiku je dN častíc, ktoré majú rýchlosti od v do v + dv. Z grafu vidno, že pravdepodobnosť nulovej rýchlosti častice je nulová, čo znamená, že pri nijakej teplote sa nezastaví tepelný pohyb častíc plynu. Tiež vidíme, že čím je teplota plynu vyššia, tým sa závislosť stáva viac  plochou  a  najpravdepodobnejšia  rýchlosť nadobúda vyššie hodnoty,  t.j. viac častíc má vysoké rýchlosti. Graf nie je symetrický, čo znamená, že najpravdepodobnejšia rýchlosť v_m nebude totožná so strednou rýchlosťou ani so strednou kvadratickou rýchlosťou  v_k.. Najjednoduchšie je získať strednú kvadratickú rýchlosť zo (4.1.4):

 

  ,            

 

odkiaľ                 

 

.

 

Potom

 

                                                                                              (4.1.25)

 

a stredná rýchlosť (príklad 4.1.8.1)

 

 

  .                                                                                           (4.1.26)

_______________________

 

Príklad 4.1.8.4  

Predstavte si, že máme plyn, častice ktorého sa môžu pohybovať len v rovine (tzv. dvojrozmerný plyn). Odvoďte vzťah analogický vzťahu (4.1.22).

 

Riešenie: 

Postupujeme úplne rovnako ako v § 4.1.8, s tým rozdielom, že konce vektorov rýchlostí nebudú v guľovej vrstve, ale v medzikruží. Pri výpočte integrálu použijeme vzorec 

 

 . 

 

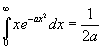Výsledný vzťah je 

 

  .

__________________________
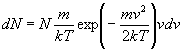