4.1. 9  Prenosové javy

Častice plynu pri chaotickom tepelnom pohybe sa premiestňujú z miesta na miesto a pri tom menia svoje rýchlosti, hybnosti a energie. Tento pohyb vedie k prenosu hmotnosti a energie z jedného miesta v nádobe na iné. Preberieme tri základné prenosové (transportné)  javy: difúziu, tepelnú vodivosť a vnútorné trenie. Majú niekoľko spoločných znakov: vo všetkých prípadoch sa prenáša nejaká veličina (hmotnosť, kinetická energia, hybnosť) dovtedy, kým táto veličina nie je rovnomerne rozdelená v celej nádobe. Všetky tieto deje prebiehajú jedným smerom, sú nevratné. Tento prenos je spôsobený tepelným pohybom častíc plynu a nie premiestňovaním väčších celkov plynu.

Prenos veličiny je možný len vtedy, ak je táto veličina rozdelená nerovnomerne. Potom ak vložíme do plynu myslenú plôšku budú cez ňu prechádzať častice oboma smermi, jedným smerom však viac. Výsledok prenosu veličiny je určený súčtom týchto protismerných tokov. Je zrejmé, že ak je veličina rozdelená rovnomerne, toky z oboch smerov cez plôšku sú rovnaké a výsledkom je nulový prenos cez plôšku. Všeobecný výpočet   nás dovedie k vzťahu

 

  .                                                                                                   (d)

 

kde b je prenášaná veličina prepočítaná na jednu časticu a n je koncentrácia častíc.

 

4.1.9.1  Difúzia

Ak na rôznych miestach máme rôzne plyny, v dôsledku tepelného pohybu dochádza k ich vzájomnému premiešavaniu, postupne sa vytvorí rovnorodá zmes častíc plynov. Jav, ktorý vedie k vzniku rovnorodej zmesi častíc plynu nazývame difúziou. My budeme uvažovať najjednoduchší prípad, keď častice plynu sa premiešavajú s časticami toho istého plynu. Tiež predpokladáme všade rovnakú teplotu, lebo v opačnom prípade by boli v nádobe miesta s rôznymi tlakmi plynu (p = nkT), čo by viedlo k makroskopickému premiestňovaniu plynu v nádobe. Teda predpokladáme, že aj tlak plynu je všade rovnaký.

Aby sme mohli pohyb častíc cez plôšku dS sledovať, označkujeme si (v našom prípade rovnaké) častice ako A a B. Častice A sa pôvodne nachádzajú v priestore 1, častice B v priestore 2, ktoré sú po oboch stranách plôšky. Keďže častice sú rovnaké, ich koncentrácie na oboch stranách plôšky sú rovnaké, za daných podmienok budú mať rovnaké stredné rýchlosti aj rovnaké stredné voľné dráhy. Pri difúzii výsledná koncentrácia častíc sa skladá z parciálnych koncentrácií, t.j.   n = n_A + n_B = const,   po diferencovaní: 0 = dn_A + dn_B , , odkiaľ  dn_A = - dn_B . Pri difúzii je prenášanou veličinou hmotnosť. Potom dB = dM_A  je hmotnosť častíc A, ktoré prešli cez plôšku dS za čas dt. Hmotnosť jednej častice je m, potom  bn₁ = mn_A . Tento súčin môžeme predstaviť ináč: m je hmotnosť jednej častice a  n je počet častíc v jednotke objemu, teda mn je hmotnosť objemovej jednotky, čo sa číselne rovná hustote r. Tieto veličiny dosadíme do všeobecného vzťahu (d) v § (4.1.9):

 

  .                                                                 (e)

 

Častice A putujú do miest, kde je ich koncentrácia nižšia, t.j. proti smeru gradientu koncentrácie (obr. 4.1.7). Ak by sme sa na difúziu pozreli zo strany častíc B, nahradili by sme dn_A   veličinou   -  dn_B  (pozri zdôvodnenie uvedené vyššie) a dostali by sme

 

  .

 

 

 

 

 

 

 

 

 

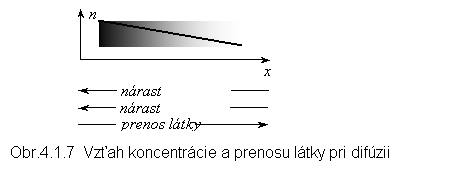
Častice B postupujú opačným smerom ako častice A a gradient ich koncentrácie má opačnú orientáciu. Za podmienok riešenia tejto úlohy je očividné, že toky častíc na obe strany sú rovnaké, dM_A = dM_B. Konštanta D sa nazýva koeficient difúzie

 

   .                                                                                                             (4.1.27)