4.1.7  Boltzmannov zákon

            Budeme sa venovať rozdeleniu častíc plynu vo vertikálnom stĺpci s prierezom S. Vyčleníme si v stĺpci vrstvu veľmi malej hrúbky a budeme uvažovať za akých okolností bude  vrstva v rovnováhe. Okrem čisto mechanických úvah musíme vziať do úvahy aj stavovú rovnicu plynov. Po výpočte  dostaneme vzťah

 

  .                                                                                             (4.1.18)

 

 

Veličina n0 je koncentrácia častíc vo výške y = 0. V čitateli je potenciálna energia jednej častice v tiažovom poli. Vidíme, že koncentrácia plynu s narastajúcou výškou exponenciálne klesá. Tiež vidíme, že tento pokles je tým rýchlejší, čím sú častice ťažšie. Napr. v atmosfére sa udržuje vodík v značných výškach, zatiaľ čo kyslík a dusík tam už takmer nie sú. Vzťah (4.1.18) sa nazýva barometrická formula. Ideálne neplatí, lebo vzduchový stĺpec nemá v každej výške tú istú teplotu. Atmosféra tak ako ju poznáme, existuje vďaka tepelnému pohybu molekúl vzduchu. Ak by tento pohyb nejestvoval, molekuly vzduchu by pod vplyvom tiažovej sily „popadali“ na povrch Zeme.

            Vzťah (4.1.18) udáva rozdelenie koncentrácie plynu, ktorého častice sa nachádzajú v poli tiažových síl. Ukazuje sa, že rovnako môžeme postupovať aj v prípade iného silového poľa, vtedy bude však potenciálna energia iná. Potenciálnu energiu si označíme Wp. Potom môžeme všeobecne napísať

 

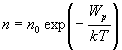   .                                                                                               (4.1.19)

 

Keďže Wp závisí od polohy častice, tento vzťah udáva koncentráciu častíc v tomto mieste. Zo vzťahu (4.1.19) vyplýva, že pri konštantnej teplote T koncentrácia častíc n narastá s ubúdaním potenciálnej energie. To znamená, že častice sa koncentrujú v miestach, kde je ich potenciálna energia menšia. Ak budeme zvyšovať teplotu, pri

T ® ¥ bude Wp / kT ® 0   a   n ® n0 ,  t.j. čím je teplota vyššia, tým menšie budú rozdiely v koncentráciách medzi susednými oblasťami v plyne, teda častice plynu budú rozdelené rovnomernejšie.  

Tento vzťah platí aj všeobecnejšie, nielen pre potenciálnu energiu, ale aj pre kinetickú Wk, aj pre súčet kinetickej a potenciálnej energie W (prirodzene predpokladáme, že častica má tieto energie a ich veľkosť závisí od miesta výskytu častice). Potom všeobecnejší tvar vzťahu (4.1.19) bude

 

   .                                                                                                (4.1.20)

 

Tento vzťah sa nazýva Boltzmannovým zákonom rozdelenia energie. Pre plyn nachádzajúci sa v rovnovážnom stave a ktorého častice podliehajú zákonom klasickej mechaniky je počet častíc s energiou W úmerný faktoru exp (-W/kT).

Vrátime sa ešte k vzťahu (4.1.18), ktorý udáva koncentráciu častíc plynu vo výške h, t.j. častíc s potenciálnou energiou Wp = m0gh. V tomto prípade ide o Wp vo výškovom intervale dy,  ktorý je vo výške h. Pravdepodobnosť výskytu častice s Wp vo vrstve hrúbky dy nachádzajúcej sa vo výške h je úmerná koncentrácii častíc a hrúbke tejto vrstvy a veličine závisiacej od Wp a T

 

   .                                                                                        

 

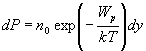Posledný vzťah môžeme zovšeobecniť a zameniť potenciálnu energiu celkovou mechanickou energiou častice W. V takýchto prípadoch bude

 

pravdepodobnosť výskytu javu  

 

   .                                                                                                       (4.1.21)

 

Tento posledný vzťah má širokú platnosť a tiež sa nazýva Boltzmannovým zákonom, ktorý hovorí, že ak je plyn v rovnovážnom stave a ak jeho častice sa riadia zákonmi klasickej mechaniky, potom pravdepodobnosť výskytu javu spôsobeného tepelným pohybom častíc je úmerná

.

 

Tento člen obsahuje napr. vzťah pre elektrický prúd termoelektrónovej emisie (elektrón v dôsledku tepelného pohybu opúšťa horúci povrch kovu), počet odparených molekúl z povrchu kvapaliny a mnohé iné vzťahy opisujúce javy, ktoré majú pôvod v tepelnom pohybe častíc látky.

_________________________

 

Príklad 4.1.7.1 

Prachové častice, ktoré majú polomer r = 2.10-7 m sa vznášajú vo vzduchu. Tlak vzduchu je 105 Pa, teplota 0 °C. Meraním sa zistilo, že vo výške h = 10 m sa koncentrácia prachových častíc znížila 2 krát. Vypočítajte hmotnosť častice.

 

Riešenie: 

Na časticu, ktorá sa vznáša pôsobia dve sily: tiaž mg a nadľahčujúca Archimedova sila FA = r0 g V , r0 je hustota vzduchu (ktorú budeme považovať za týchto podmienok konštantnú), V je objem častice. Objem častice si vyjadríme ako  V = m/p, kde m je hmotnosť častice a r je jej hustota. Potom FA = mg (r0/r) a celková sila pôsobiaca na časticu je

 

.

 

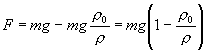Potenciálna energia častice (v silovom poli vytváranom tiažovými a nadľahčujúcimi silami) vo výške y je

 ,

 

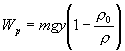čo dosadíme do (4.1.18)

 

 , 

 

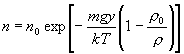kde n je koncentrácia prachových častíc vo výške y a n0 tesne nad povrchom zeme. Ak y = 10 m, je  n = n0/2.

 

Takže máme

 

 ,

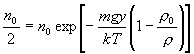odkiaľ 

 

.

 

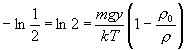Hustota častice je

 

 ,          

 

takže

 ,

 

odkiaľ už môžeme vypočítať hmotnosť prachovej častice pomocou zadaných veličín. Potrebujeme ešte hustotu vzduchu r0. Podľa tabuliek r0 = 1,276 kg/m3. Po dosadení číselných hodnôt dostaneme m = 5,4.10-21 kg.

____________________________