Práca, ktorú
vykonáme pri premiestnení náboja q
v elektrostatickom poli E na úseku
dr je
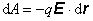 (6.1.75)
(6.1.75)
Teda
 (6.1.76)
(6.1.76)
Elektrostatický potenciál j je vo všeobecnosti funkciou súradníc x, y, z. V I. kapitole o vektorovom počte sme ukázali, že
diferenciálnu zmenu skalárnej funkcie priestorových súradníc x, y, z možno vyjadriť
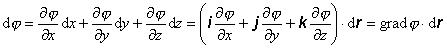 (6.1.77)
(6.1.77)
Porovnanie rovníc (76) a (77)
ukazuje, že platí vzťah
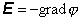 (6.1.78)
(6.1.78)
To znamená, že ak poznáme
potenciál j (x,
y, z), tak potom vieme
v každom bode vypočítať intenzitu
poľa E( x , y, z) pomocou vzťahu
(6.1.78). Z rovnice (6.1.77) vyplýva, že ak vektor posunutia dr bude kolmý na gradj tak dj = 0. To
znamená, že vektor posunutia dr v tomto prípade leží na ploche
konštantného potenciálu j . Tým sa dostávame k dôležitému poznatku, že vektor E je v každom bode kolmý na ekvipotenciálnu hladinu, ktorá týmto bodom
prechádza.
Príklad 6.1.10.4
Vychádzajúc z potenciálu 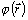 bodového náboja
umiestneného v začiatku súradnicového systému ukážte, že záporne vzatý
bodového náboja
umiestneného v začiatku súradnicového systému ukážte, že záporne vzatý 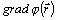 je totožný
s elektrostatickým poľom.
je totožný
s elektrostatickým poľom.
Riešenie:
Potenciál bodového náboja q, ktorý sa nachádza
v bode (0, 0, 0) je
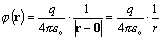 (1)
(1)
Elektrické pole v okolí tohoto náboja určíme
nasledovne
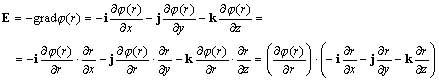
kde musíme funkciu j (r
) derivovať ako zloženú funkciu. Funkcia
j je podľa rovnice (1) formálne
funkciou jedinej premennej r , a preto môžeme písať
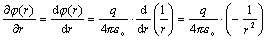
Parciálna derivácia r podľa súradnice x je
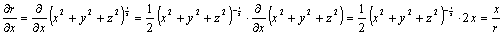
Podobne dostaneme
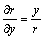
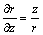
Teda

__________________________________________________________________________________