Vzťah
(6.1.69), ktorý sme dostali pre potenciál bodového náboja môžeme na základe princípu
susperpozície elektrických polí ihneď zovšeobecniť na ľubovoľnú sústavu
bodových nábojov qi :
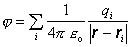 (6.1.71)
(6.1.71)
Pre spojité
rozloženia nábojov s hustotou r(r´) máme

 (6.1.72)
(6.1.72)
a integrácia prebieha cez celý
objem V, kde sa nachádzajú náboje.
Pre náboje rozložené na ploche s plošnou hustotou s platí
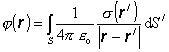 (6.1.73)
(6.1.73)
A pre náboje
rozložené na vlákne s dĺžkovou hustotou l pozdĺž nejakej krivky C je
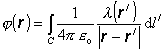 (6.1.74)
(6.1.74)
Vidíme, že
vzťahy na výpočet potenciálu sú podstatne jednoduchšie ako vzťahy na výpočet
elektrostatického poľa, čo sa v praxi veľmi často aj využíva. Potrebujeme nájsť
len obrátený "recept" na
výpočet elektrického poľa ak poznáme potenciál, čo bude predmetom nasledujúceho
odseku.
___________________________________________________________________________
Príklad 6.1.10.1 Dva bodové
náboje 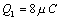 ,
, 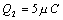 sú vo vzdialenosti d = 20 cm. V ktorom mieste na
ich spojnici sú potenciály budené oboma nábojmi rovnaké?
sú vo vzdialenosti d = 20 cm. V ktorom mieste na
ich spojnici sú potenciály budené oboma nábojmi rovnaké?
|
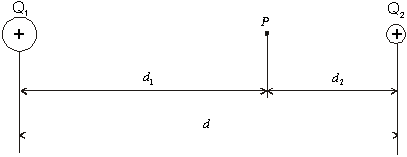
Obr.6.1.10.1
|
Riešenie: Potenciál bodového
náboja 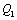 v bode P sa rovná
v bode P sa rovná
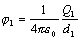 ,
,
potenciál bodového náboja  v bode P sa rovná
v bode P sa rovná
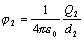 .
.
Potenciály sú rovnaké, čo
znamená
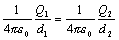 ,
,
po úprave a dosadení 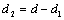 dostaneme
dostaneme

Potenciál je rovnaký vo
vzdialenosti 12 cm od väčšieho náboja.
Príklad 6.1.10.2 Vo vrcholoch štvorca so
stranami 10 cm sú umiestnené 4 rovnako veľké náboje s veľkosťou 10-7
C. Určite potenciál v strede štvorca, ak znamienka nábojov q1 , q2
, q3, q4 sú
a) ++++
b) + - + -
c) + + - -
|
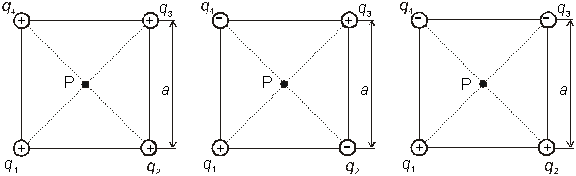
a) b) c)
Obr.6.1.10.2
|
Riešenie“: Vzdialenosť vrcholu od stredu štvorca P je
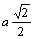 .Potenciál bodového náboja v tejto vzdialenosti vypočítame
podľa vzťahu
.Potenciál bodového náboja v tejto vzdialenosti vypočítame
podľa vzťahu  .
.
Na základe princípu superpozície elektrických polí
potenciál 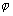 v bode P dostaneme ako súčet potenciálov od 4 bodových
nábojov.
v bode P dostaneme ako súčet potenciálov od 4 bodových
nábojov.
a) 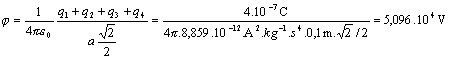
b) 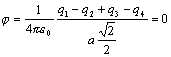
c) 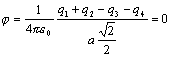
Potenciál v strede štvorca je a) 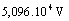 , b)
, b)  , c)
, c) 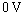 .
.
_________________________________________________________________________________
Príklad 6.1.10.3 Dve veľmi
dlhé kovové valcové plochy sú súosé. Polomer vnútornej valcovej plochy je r1
, polomer vonkajšej je r2 . V priestore medzi nimi je
vákuum. Na valcové plochy privedieme náboj tak, že ich pripojíme k zdroju
napätia U. Po odpojení zdroja vonkajšiu plochu uzemníme. Vyšetrite potenciál
elektrostatického poľa medzi plochami.
Riešenie:
|
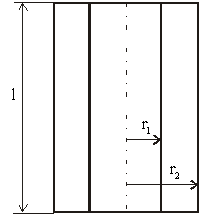
Obr.
6.1.10.3
|
Z Gausovej vety platí
pre intenzitu poľa medzi valcovými plochami:
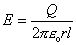

kde Q je náboj na vnútornej ploche, l je dĺžka valca a r je vzdialenosť
od osi valca. Pritom platí r1
<
r < r2 . Pre elektrostatický potenciál
vo všeobecnosti platí
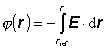
kde rref je polohový vektor bodu, na ktorý vzťahujeme
potenciál. V našom prípade to bude uzemnená vonkajšia valcová plocha. Keďže
pri výpočte potenciálu výsledná hodnota nezávisí od konkrétnej integračnej
cesty, budeme ju voliť kolmo na os valca, takže v tomto prípade bude vždy E
dr . Potom sa nám výpočet potenciálu zjednoduší:

Špeciálne pre r = r1 a r = r2 dostaneme
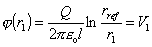
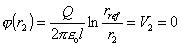
nakoľko rref
= r2 . V našom prípade je
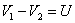
z čoho potom
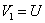
Pri známom l možno
vypočítať náboj Q
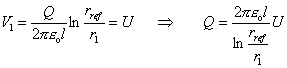
Pre potenciál vo
vzdialenosti r od osi valca potom dostaneme