Quantum Mechanics - 3

Molecular Orbitals

In the previous Section, we discussed a method for solving the Electronic Schrödinger Equation for a system of one electron. For systems of many electrons, finding solutions is more difficult. One also has to find a way to represent the dependence of the wavefunction on all the coordinates. A common way of doing this (at least as a starting point) involves the use of yet another approximation, the (Molecular) Orbital Approximation. This consists in writing the wavefunction as a product of one electron wavefunctions:

\[ \Psi(r_1,r_2,\ldots r_n)=\prod_{i=1}^{n}\psi_i(r_i) \;\;\; [\text{that is,} \;\; \psi_1(r_1)\psi_2(r_2)\ldots \psi_n(r_n) ] \]

These one-electron wavefunctions are also called Orbitals, and, in the case of molecules, are generally approximately expanded in a basis set of atomic functions:

\[ \psi_i(r)=\sum_{j=1}^{n_{basis}}c_{ij}\phi_j(r) \]

The molecular orbital approximation is equivalent to assuming that the electrons behave independently from each other. The probability of finding an electron in orbital i at a given place ri does not depend on where the other electrons are:

\[ P(e_i,r_i)=\psi_i^2(r_i)\int \left \{ \prod_{j \neq i} \psi^2_j(r_j) \right \} \; dr = \psi_i^2(r_i) \]

As a result, the probability of finding ANY electron at a given point in space is just the sum of the probabilities of finding one there in each of the orbitals.

Although we will not discuss this at length, the Orbital Approximation is equivalent to assuming that the electronic Hamiltonian can be expressed as a sum of one-electron hamiltonians:

\[ \hat{H}_{elec} \approx \sum_{i=1}^{n}h_{elec}^{i} \]

For comparison, the full, correct electronic Hamiltonian is shown below. As can be seen, the first and second terms, which correspond to the kinetic energy of individual electrons, and to the interaction of each electron with the nuclei, respectively, are indeed sums over all the electrons. By contrast, the final term, which corresponds to the repulsion between electrons, cannot be separated in this way. This already gives an indication that expressing wavefunctions as products of molecular orbitals (the Molecular Orbital Approximation) involves making an approximation to how the electrons interact with each other. For more details, see the section on the Hartree-Fock Method.

\[ \hat{H}_{elec}= \sum_{i=1}^{n} {\frac{-\nabla_i^{2}}{2}} + \sum_{i}^{n}\sum_{A}^{N} \frac{-Z_{A}}{r_{iA}} + \sum_{i}^{n}\sum_{j>i}^{n} \frac{1}{r_{ij}} \]

As an example, the wavefunction of the Boron atom (Z = 5) in its ground state can be written in the following way:

\[ \Psi(\mbox{B}) = \psi_{1s}(r_1)\psi_{1s}(r_2)\psi_{2s}(r_3)\psi_{2s}(r_4)\psi_{2p}(r_5) \]

This sort of expression, which gives the electronic configuration of an atom or a molecule, is often written in shorthand in the following way:

\[ \Psi(\mbox{B}) = \mbox{1s}^2\mbox{2s}^2\mbox{2p}^1 \]

Molecular Orbitals and Symmetry

The s and p labels above are Symmetry Labels - they indicate the type of symmetry of each molecular orbital. You will have learnt in the Chemical Applications of Group Theory Unit given by Dr. Norman that each molecule (or atom) can be characterised by a certain overall symmetry in the way the nuclei are positioned. This is called the Point Group to which the molecule belongs. Some examples are $\mbox{D}_{\infty h}$ , $\mbox{C}_{2v}$ , etc. You will also have learnt that to each point group, there corresponds a certain number of Symmetry Operations, such as rotation round an axis, reflection through a plane, inversion through a center of symmetry, which leave the molecule overall unchanged.

In general, the molecular orbitals are chosen to be either Symmetric or Antisymmetric with respect to each of the symmetry operations. Depending on the details of which operations they are symmetric to and which they are antisymmetric to, they have a certain Symmetry Label (Or, equivalently, they are said to belong to a given Irreducible Representation of their Point Group.).

You are already well familiar with the names of the irreducible representations of the point group to which atoms belong: s, p, d, f, ...

In Year 2, you also learnt about the irreducible representations of linear molecules: sigma, pi, delta, ... So the wavefunction for molecular nitrogen, N2, is written:

\[ \Psi(\mbox{N}_2)=\psi^2_{1\sigma_g}\psi^2_{1\sigma_u} \psi^2_{2\sigma_g}\psi^2_{2\sigma_u}\psi^4_{1\pi_u}\psi^2_{3\sigma_g} \]

Remember that homonuclear diatomic molecules are symmetric with respect to inversion through the center of the molecule. Therefore, their orbitals have to be either symmetric (g) or antisymmetric (u) to inversion of the two atoms, whereas heteronuclear diatomics such as CO do not have this symmetry so their orbitals do not have g or u labels.

In general, polyatomic molecules can belong to any of the different point groups. Let us examine in some more detail the wavefunction of the water molecule, which has $\mbox{C}_{2v}$ symmetry:

\[ \Psi\{\mbox{H}_2\mbox{O}\} = \psi_{1a_1}^2\psi_{2a_1}^2 \psi_{1b_2}^2\psi_{3a_1}^{2}\psi_{1b_1}^2 \]

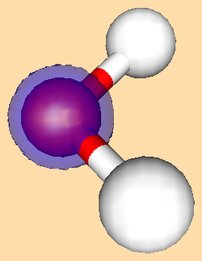
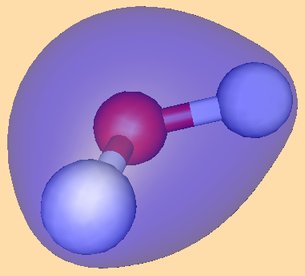
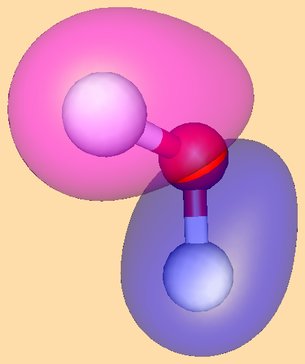
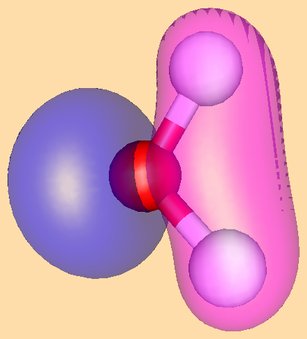
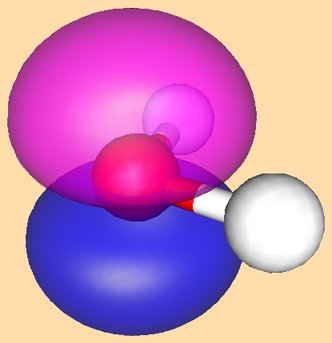
Below is a Table with cartoons of the molecular orbitals, their symmetry, and the coefficients (cij) of the atomic orbitals which make them up:

 
         (A1)--O 
O  1S    0.99423 
   2S    0.02571 
   2PX   0.00000 
   2PY   0.00000 
   2PZ  -0.00393 
H  1S   -0.00552 
H  1S   -0.00552 

 
         (A1)--O 
O  1S   -0.23458 
   2S    0.84943 
   2PX   0.00000 
   2PY   0.00000 
   2PZ  -0.11468 
H  1S    0.15539 
H  1S    0.15539 

 
         (B2)--O 
O  1S    0.00000 
   2S    0.00000 
   2PX   0.00000 
   2PY   0.60478 
   2PZ   0.00000 
H  1S    0.44732 
H  1S   -0.44732 

 
         (A1)--O 
O  1S   -0.10047 
   2S    0.52067 
   2PX   0.00000 
   2PY   0.00000 
   2PZ   0.76891 
H  1S   -0.29415 
H  1S   -0.29415 

 
         (B1)--O 
O  1S    0.00000 
   2S    0.00000 
   2PX   1.00000 
   2PY   0.00000 
   2PZ   0.00000 
H  1S    0.00000 
H  1S    0.00000

Roughly speaking, the first a1 orbital is the 1s orbital on Oxygen, and is non-bonding. The next a1 orbital is partly non-bonding, of O 2s character, and partly bonding between O and H, for which it can be though of as being a linear combination of the two sigma bonds you are familiar with. The next orbital is of b2 symmetry, and corresponds to the other linear combination of the two O-H bonds. The final orbitals correspond to two O lone pairs - one of roughly sp2 symmetry, which is partly bonding between O and H, and one of pi symmetry.

Molecular orbitals can be a help in understanding 1. Bonding and 2. Reactivity.

1. The regions of space where the amplitude of molecular orbitals is large can often be understood in terms of non-bonding core electrons, non-bonding lone-pairs, bonding and anti-bonding - as we have done above for water. The electronic structure of formaldehyde will be analysed in the same way in a Workshop after the end of this lecture unit. Note that the fact the orbitals are molecular - and are thus delocalised over the whole molecule can be a bit confusing at first if you are used to thinking in terms of Lewis Structures (localised lone pairs and bonding pairs).

To understand how MOs help understand reactivity, you need to know what happens to orbitals of different fragments when they approach: they mix with orbitals on the other fragment to form new orbitals for the whole system. Several important rules govern this mixing:

You can use this analysis in terms of fragment orbitals can be used to understand how atoms come together to form molecules. You have already done this for diatomic molecules (Year II - Prof. Ashfold course) & You will do it to analyse the bonding orbitals of water in a practical exercise this year (Symmetry Aspects of Molecular Electronic Structure Dr. Allan).

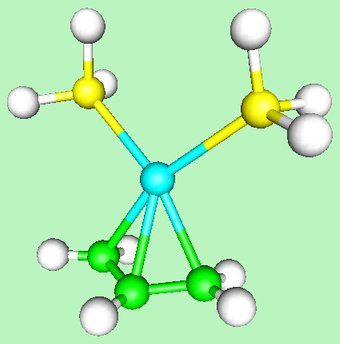
Here is more advanced example, concerning the electronic structure of cationic Allyl- Palladium complexes. These species are formed by the attack of Pd(0) compounds on allyl halides and are important intermediates in the Tsuji-Trost allylic substitution reaction. The structure of the parent compound is shown here (note the plane of symmetry):

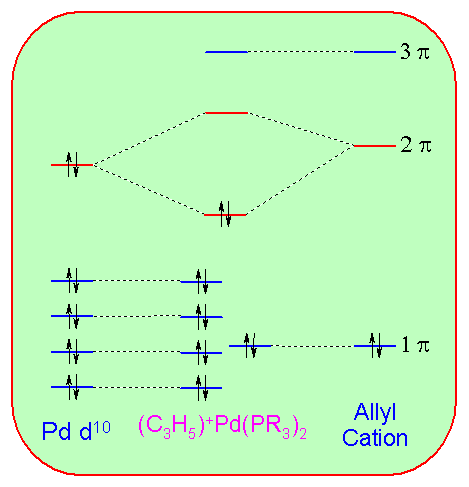
The bonding interaction between the Pd(PR3)2 moiety and the allyl cation can be understood with the following diagram:

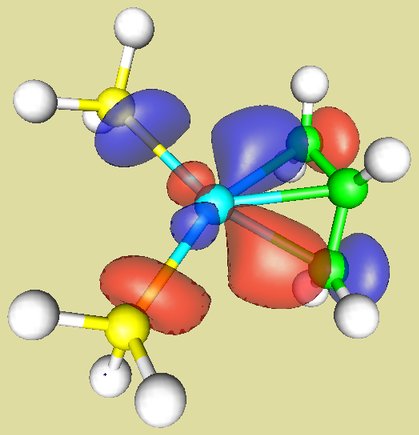
The HOMO of Pd(PR3)2 and the LUMO of allyl cation as they approach one another are shown here (note that both are antisymmetric with respect to the plane of symmetry):

And the HOMO of the complex is shown here:

For reactivity, the rules given above mean that chemical reactions tend to have low barriers only if their "Frontier" orbitals - the Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO) meet certain conditions:

The analysis of reactivity with these rules forms the basis of so-called Frontier Molecular Orbital (FMO) theory, which is strongly related to the Woodward-Hoffmann rules, which you have met in Organic Chemistry lectures and in Dr. Mulholland's Year 2 Unit.

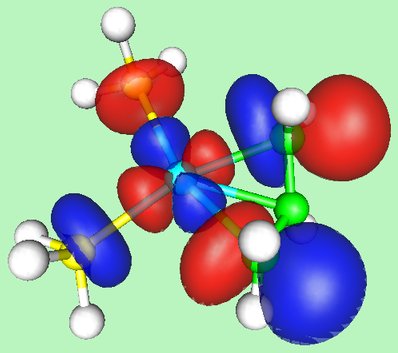
For two examples of applications, see (1) the Tungsten carbene complex discussed in the Introductory Section, and (2), consider the following LUMO of the Tsuji-Trost intermediate discussed above:

Click here to return to the list of online lectures

Click here to return to the previous Section

Click here to go on to the next Section

This page created by Jeremy Harvey, Bristol, 2000.