Quantum Mechanics - 2

The Variational Method

The problem in theoretical and computational studies of Molecular Electronic Structure is to solve the electronic Schrödinger equation for a system of N nuclei and n electrons:

\[ \hat {H}_{elec} \Psi (r)=E_{elec}\Psi (r) \]

\[ \hat{H}_{elec}= \sum_{i=1}^{n} {\frac{-\nabla_i^{2}}{2}} + \sum_{i}^{n}\sum_{A}^{N} \frac{-Z_{A}}{r_{iA}} + \sum_{i}^{n}\sum_{j>i}^{n} \frac{1}{r_{ij}} \]

The Schrödinger Equation has analytical solutions for some simple systems:

In most cases, one needs instead to use Numerical approaches. For the most part, these rely upon the Variational Principle, and involve the use of a basis-set and of linear algebra instead of differential calculus.

To understand how these methods work, it helps to consider how one solves the Schrödinger equation for a one-particle system.

The basis set here is a set of basis functions depending on the coordinates of the particle. Linear combinations of the basis functions can be used to approach ANY given function of those coordinates.

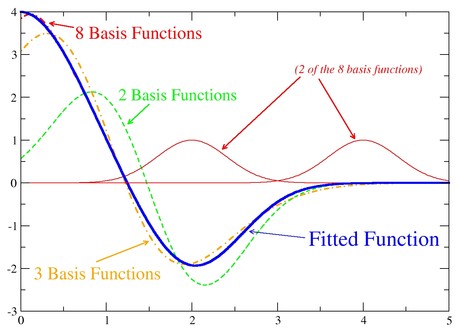
sums of basis functions to represent a function

In the case of the Schrödinger equation, the following expression can be used as an approximation to the correct eigenfunction:

\[ \Psi \{r\} \approx \sum_{i=1}^{n_{basis}} c_{i}\phi_{i}(r) \;\;\;\; \left [ \text{that is,} \;\; c_{1}\phi_{1} + c_{2}\phi_{2} + \ldots c_{n}\phi_{n} \right ] \]

How can one find the coefficients ? This is where the Variational Principle comes in: The ci which give the best wavefunction are those which give the lowest energy.

This leads to a set of n equations, called the Secular Equations, giving the n solutions to the Schrödinger equation with n basis functions:

\[ \left \{ \begin{array}{l} c_{1}(H_{11}-ES_{11})+c_{2}(H_{12}-ES_{12})+\ldots c_{n}(H_{1n}-ES_{1n})=0\\ c_{1}(H_{21}-ES_{21})+c_{2}(H_{22}-ES_{22})+\ldots c_{n}(H_{2n}-ES_{2n})=0\\ c_{1}(H_{31}-ES_{31})+c_{2}(H_{32}-ES_{32})+\ldots c_{n}(H_{3n}-ES_{3n})=0\\ \vdots\\ c_{1}(H_{n1}-ES_{n1})+c_{2}(H_{n2}-ES_{n2})+\ldots c_{n}(H_{nn}-ES_{nn})=0 \end{array} \right. \]

The Sij and Hij terms are called matrix elements and are given by:

\[ S_{ij}=\int \phi_i(r)\phi_j(r) dr \]

\[ H_{ij}=\int \phi_i(r)\hat{H}\phi_j(r) dr \]

These n equations form what is called a set of homogeneous equations, which always have at least one, trivial solution, i.e. ci = 0. Under certain conditions, however, there are an additional n solutions cij (j = 1, n). The lowest energy solution is given by the ci1, with the other solutions corresponding to excited states.

Note that the equations can be written much more concisely:

\[ \sum_{i=1}^{n}c_{ij}\{H_{ij}-ES_{ij}\}=0 \;\;\;(j=1,n) \]

Or, in matrix form:

\[ \mathbf{HC-ESC}=0 \]

By solving this system of simultaneous homogeneous equations, one will obtain a set of n possible possible values of E, and n corresponding sets of coefficients c. To do this, one uses the mathematical property that the determinant of the matrix C formed by the coefficients of the equations must be equal to 0 for a solution to exist:

\[ \left | \begin{array}{ccccc} H_{11}-ES_{11} & H_{12}-ES_{12} & H_{13}-ES_{13} & \cdots & H_{1n}-ES_{1n} \\ H_{21}-ES_{21} & H_{22}-ES_{22} & H_{23}-ES_{23} & \cdots & H_{2n}-ES_{2n} \\ H_{31}-ES_{31} & H_{32}-ES_{32} & H_{33}-ES_{33} & \cdots & H_{3n}-ES_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ H_{n1}-ES_{n1} & H_{n2}-ES_{n2} & H_{n3}-ES_{n3} & \cdots & H_{nn}-ES_{nn} \\ \end{array} \right | = 0 \]

Solving this can be done 'by hand' for small systems. For larger determinants, this is impossible. Instead, one performs what is called a diagonalisation of the matrix of coefficients, and extracts a set of n eigenvalues (solutions for E) and n corresponding eigenvectors (solutions for the ci).

So for systems with one particle (e.g. one electron), it is easy to choose a suitable basis set and solve the Schrödinger equation. With some further approximations, some many-electron problems can be treated as single-electron system, and solved in the way discussed here. This is what is done in Hückel Molecular Orbital Theory for conjugated hydrocarbons, which you studied with Dr. Mulholland in Year 2.

Click here to return to the list of online lectures

Click here to return to the previous Section

Click here to go on to the next Section

This page created by Jeremy Harvey, Bristol, 2000.