![\[ i\hbar \frac{\partial \Xi(r,t)} {\partial t} = \hat {H} \Xi(r,t) \]](formulas/schrodinger_1.gif)
Within quantum mechanics, chemical systems are treated as physical systems, and their behaviour is predicted by the fundamental laws of physics. In short:
Molecule = Nuclei + Electrons
And the "elementary" particles are described by their mass, their electrical charge, their magnetic properties, ...
Such systems are described by the Time-dependent Schrödinger equation:
![\[ i\hbar \frac{\partial \Xi(r,t)} {\partial t} = \hat {H} \Xi(r,t) \]](formulas/schrodinger_1.gif)
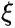 is the Wavefunction, which describes the state of the system throughout
space (position of the particles, r) and time.
H is the Hamiltonian Operator, which describes how the system changes in time.
is the Wavefunction, which describes the state of the system throughout
space (position of the particles, r) and time.
H is the Hamiltonian Operator, which describes how the system changes in time.
For many systems, the time-dependence only contributes an unimportant phase factor:
![\[
\Xi(r,t)=\Theta(r) e^{-iEt/\hbar} \]](formulas/schrodinger_2.gif)
Where E is the energy of the system. Substituting this expression into the Schrödinger equation, above, yields the following:
![\[
i\hbar \frac{\partial \Xi} {\partial t} =
i\hbar \times \Theta(r) \times e^{-iEt/\hbar} \times \frac {-iE}{\hbar}
=E \times \Theta(r) e^{-iEt/\hbar} \]](formulas/schrodinger_3.gif)
This equation can be separated into two. The most important of the equations from our point of view deals only with the space-dependent part of the wavefunction:
![\[
\hat {H}\Theta(r) = E\Theta(r) \]](formulas/schrodinger_4.gif)
Even so, the wavefunction is a very complex construct:
![\[
\Theta \left \{ R_{1},R_{2},\ldots R_{N},r_{1},r_{2},r_{3},\ldots r_{n} \right \} \]](formulas/schrodinger_5.gif)
To take an example, the wavefunction for a benzene molecule depends on 54 variables: 3 Cartesian coordinates each for 6 Carbon nuclei, 6 Hydrogen nuclei, and 6 x 6 + 6 x 1 electrons.
The Hamiltonian Operator acts on all these variables, and mixes them up in a complicated way, because it depends on the inter-particle distances:
![\[
\hat {H} = \sum_{i=1}^{n} {\frac{-\nabla_i^{2}}{2}} + \sum_{A=1}^{N} \frac {-\nabla_A^{2}}
{2 M_{A}} + \sum_{i,j>i}^{n} \frac{1}{r_{ij}}
+ \sum_{A,B>A}^{N}\frac{Z_{A}Z_{B}}{R_{AB}}+\sum_{i,A}^{n,N} \frac{-Z_{A}}{r_{iA}}
\]](formulas/schrodinger_6.gif)
Again, to take the example of benzene, there are 42 x 41 / 2 = 861 electron-electron distances!
This first step in simplifying the equation is based on the fact that nuclei are much more heavy than electrons. This means that on the timescale where electrons move around, the nuclei are essentially fixed. Under these conditions, it is possible to factorise the wavefunction:
![\[ \Theta \{R,r\} = \Psi\{r,\underline{R}\}\Omega \{R\} \]](formulas/schrodinger_7.gif)
In other words, the total wavefunction can be written as a product of two functions,
one (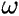 ) which depends only on the positions of the nuclei, and one (
) which depends only on the positions of the nuclei, and one (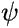 ) which
depends on the positions of the electrons, but is also parametrically dependent
on the positions of the nuclei (shown symbolically in the formula by underlining R).
This means that the function does not contain any terms explicitly
dependent on R, but that there is a different function for each set of R.
) which
depends on the positions of the electrons, but is also parametrically dependent
on the positions of the nuclei (shown symbolically in the formula by underlining R).
This means that the function does not contain any terms explicitly
dependent on R, but that there is a different function for each set of R.
Factorising in this way leads to separating the Schrödinger equation into two separate equations, one for the electrons, and one for the nuclei. There are also two Hamiltonians. The electronic Hamiltonian is of the form:
![\[ \hat{H}_{elec}= \sum_{i=1}^{n} {\frac{-\nabla_i^{2}}{2}}
+ \sum_{i}^{n}\sum_{A}^{N} \frac{-Z_{A}}{r_{iA}}
+ \sum_{i}^{n}\sum_{j>i}^{n} \frac{1}{r_{ij}} \]](formulas/schrodinger_8.gif)
And the corresponding equation is:
![\[ \hat {H}_{elec} \Psi (r)=E_{elec}\Psi (r) \]](formulas/schrodinger_9.gif)
For the nuclei, the Hamiltonian look like this:
![\[ \hat {H}_{nucl} = \sum_{A=1}^{N} \frac {-\nabla_A^{2}}
{2 M_{A}} + \sum_{A}^{N}\sum_{B>A}^{N}
\frac{Z_{A}Z_{B}}{R_{AB}} + \int_{r}\Psi(r,R)\hat {H}_{elec}\Psi(r,R) dr \]](formulas/schrodinger_10.gif)
The last term in this expression gives the value of the electronic energy of the system for a given position of the nuclei, and is expressed as an average over the positions of all the electrons.
In the nuclear Hamiltonian, one term (the first) corresponds to the kinetic energy of the nuclei, whereas the two others are potential terms. For this reason, they can be grouped as follows:
![\[ \hat {H}_{nucl}= \sum_{A=1}^{N} \frac {-\nabla_A^{2}}{2 M_{A}} + V(R) \]](formulas/schrodinger_11.gif)
The motion of electrons almost always needs to be understood in a quantum-mechanical way. Nuclei, on the other hand, can often be thought to behave in a classical way. The time-dependent version of the nuclear Schrödinger equation often reduces to something very similar to Newtonian dynamics - the motion of a point on a surface:
 |
Solving the Electronic Schrödinger Equation Provides the Potential V upon which Molecules Vibrate and React |
Click here to return to the list of online lectures
Click here to return to Section 0.
Click here to go to the next Section.