The Pauli Principle and Spin

1. Elementary Particles Cannot be Told Apart

In previous pages, we have been writing electronic wavefunctions as Products of 1-electron functions, or molecular orbitals (these products are called Hartree products). In fact, such expressions violate a very fundamental principle of quantum mechanics: like elementary particles are indistinguishable from each other; You can't tell one electron from another. Consider a two-electron wavefunction (written as in the previous pages):

\[ \Psi(r_1,r_2)=\psi_1(r_1) \times \psi_2(r_2) \]

This is not a valid expression, because it is not the same as the indistinguishable:

\[ \Psi(r_2,r_1)=\psi_1(r_2) \times \psi_2(r_1) \]

To put this in a more graphical way, imagine we have a water molecule, and we know that such and such an electron is in the HOMO, and we then ionise the molecule as shown:

We would know which electron had been removed, whereas the indistinguishability of particles tells us we cannot know that - only that we have removed one of the 10 electrons on the water molecule.

So how should one write wavefunctions, preserving the spirit of them being products of molecular orbitals ? The answer is to take sums of products, switching the position of the electrons from one to another.

For the two-electron wavefunction, this gives:

\[ \Psi(r_{1},r_{2})=\psi_{1}(r_{1})\psi_{2}(r_{2}) + \psi_{1}(r_{2})\psi_{2}(r_{1}) \]

Experimentally, all observations depend on the square of the wavefunction, so we could in fact also take the following wavefunction:

\[ \Psi(r_{1},r_{2}) = \psi_{1}(r_{1})\psi_{2}(r_{2}) - \psi_{1}(r_{2})\psi_{2}(r_{1}) \]

For this wavefunction,

\[ \Psi(r_2,r_1) = -\Psi(r_1,r_2) \;\;\; \mbox{ (prove it !)} \]

Which means that from the point of view of observation, indistinguishability is achieved:

\[ \Psi^2(r_2,r_1) = \Psi^2(r_1,r_2) \]

It is an experimental fact that for electrons, only the second type of wavefunction, which changes sign upon exchanging the two particles, is possible. This observation leads to the Pauli Principle:

Valid Electronic Wavefunctions must change sign upon exchanging the coordinates of any two electrons.

How does this affect our picture of molecular orbitals ? Consider the wavefunction for the Helium atom, which we "know" has two electrons in the 1s orbital:

\[ \Psi(\mbox{He}) = \psi_{1s}(r_1)\psi_{1s}(r_2)-\psi_{1s}(r_2)\psi_{1s}(r_1)=0 \;\mbox{!!} \]

Electron Spin

The paradoxical conclusion at the end of the previous paragraph is due to our neglect up till now of Electron Spin. We have been assuming that electrons are fully described in terms of their position in space, their speed and their charge which undergoes Coulombic interactions with other charged particles. This leads to writing electronic wavefunctions as functions of their position only:

\[ \psi(e^-)=\psi(x_{e^-},y_{e^-},z_{e^-})=\psi(r) \]

In fact, this is not true. Experiment shows that electrons have intrinsic magnetic properties, which can be shown by passing a beam of electrons through a magnetic field. In classical physics, magnetism arises from (rotational or other) motion of charged particles. Because the electrons have intrinsic magnetic properties, i.e. they have these properties whatever they are doing, and even when they are apparently at rest, the properties have been attributed to a mysterious spinning motion of the electrons, referred to simply as spin. However, this word is only used by analogy to classical physics; as a particle which has zero size, electrons cannot really "spin" so the name should not be taken too literally. Spin is a quantum-mechanical property.

To fully describe an electron, you need a fourth coordinate, omega, so that wavefunctions should be written as:

\[ \chi(e^-)=\chi(x_{e^-},y_{e^-},z_{e^-},\omega_{e^-})=\chi(r,\omega) =\chi(\mbox{x}) \]

The spin coordinate is very unusual, and corresponds to nothing in classical mechanics. For our purposes, it is enough to say that all wavefunctions can be written in one of the following forms:

\[ \chi(\mbox{x}) = \chi(r,\omega)= \;\;\mbox{either of:} \;\; \left \{ \begin{array}{l} \psi(r) \times \alpha(\omega) = \psi(r)\alpha =\psi(r) \\ \mbox{ } \\ \psi(r) \times \beta(\omega) =\psi(r)\beta = \overline{\psi(r)} \end{array} \right. \]

The function psi is similar to the orbitals we have been writing before, and gives all the space dependence; it is often called a Spatial Orbital. There are just two possible "functions" giving the dependence on the spin coordinate, alpha and beta, which correspond classically to the electron spinning clockwise or anticlockwise, to the spin being "up" or "down". The spin "coordinate" omega is often omitted. The product of the spatial orbital and the spin function, here written as chi, is often called a Spin Orbital.

The wavefunction which must satisfy the antisymmetry requirement of the Pauli principle is the total wavefunction, with spin. This will be based on a product of one-electron orbitals 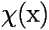$ \chi(\mbox{x}) $ . For example, the wavefunction of Helium will be of the form:

\[ \Psi(\mbox{He})(\mbox{x}_1,\mbox{x}_2)=\chi_1(\mbox{x}_1)\chi_2(\mbox{x}_2) -\chi_1(\mbox{x}_2)\chi_2(\mbox{x}_1) \]

Unlike the expression a few pages up, this does not reduce to zero even if both electrons are placed in the same 1s spatial orbital, providing the spin part of the orbitals is different:

\[ \left \{ \begin{array}{ll} \chi_1 = \psi_{1s}(r)\alpha\\ \chi_2 = \psi_{1s}(r)\beta \end{array} \right. \]

Had we tried to put both electrons into the same spatial orbital and to give them the same spin, the function would be equal to zero (prove it !), which is impossible. This observation leads to more familiar expressions of the Pauli Principle:

Some Consequences

Writing wavefunctions as an antisymmetrised sum (difference) of terms may seem to be be no big deal - all the terms look alike, after all. Actually, the consequences are rather important:

First, as discussed above, the "rule" that only two electrons may be in any given orbital is only due to spin and the Pauli Principle. Without this, all the electrons of every atom would be in 1s-like orbitals and Chemistry would not happen.

A more sophisticated conclusion can be drawn from the following simple example. Imagine you have two particles (e.g. electrons) in a box, and that one is in the ground state, the other in the first excited state. The square of the corresponding one-particle wavefunctions are shown here:

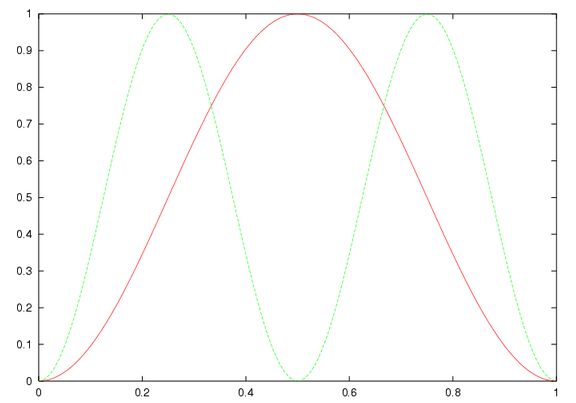
What happens to the two-electron wavefunction? Below are shown two different 2d-plots of the square of the wavefunction. The first assumes it to be a simple product of the two one-electron wavefunctions:

This is of course incorrect! The next takes it to be the correct antisymmetrised difference of products:

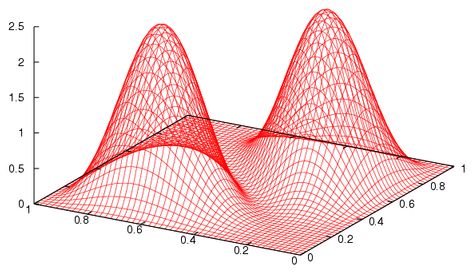
Note the differences !!!

You can easily prove that the probability of finding two electrons with the same spin at the same point in space is zero - this is not the case if the electrons have opposite spin. Although the real reason is a bit more complicated, this is the gist of the reason behind Hund's rule that electrons tend to prefer to have parallel spins: Electrons with the same spin keep away from each other better than those of opposite spin, thus minimising Coulombic repulsion.

This is very important in Transition Metal Chemistry, among others. Transition metals have a partly filled d shell - they have less than 10 electrons in 5 orbitals which are degenerate. If you use spectroscopy to study an isolated TM atom or ion, it always has a high-spin:

In the presence of ligands, some of the orbitals are more stabilised than others, but they remain fairly close in energy. Depending on the ligands, it is more favourable for the electrons to "pair up" or to remain with parallel spin.

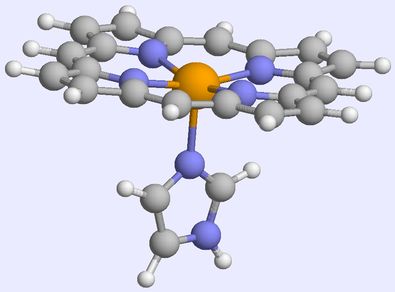
As an example, consider haem, the cofactor responsible for carrying oxygen around the body. As a free cofactor, it has a quintet ground state (4 unpaired electrons, see above). Upon binding to CO (carbon monoxide is a poison because it binds very strongly to haem), the splitting between the orbitals increases, and a ground state singlet, with the 6 d electrons paired up, is obtained:

Slater Determinants

Wavefunction need to be written as antisymmetrised products of spin-orbitals:

\[ \Psi(\mbox{x}_1,\mbox{x}_2,\ldots \mbox{x}_2)= \mathcal{A} \{ \prod_{i=1}^{n_{elec}} \chi_i(\mbox{x}_i) \} \]

We have already seen that the antisymmetrisation operator $\mathcal{A}$ means that one needs to take the difference of two related Hartree products of orbitals for a 2 electron system. For an n-electron system, the wavefunction needs to be antisymmetric with respect to interchange of any pair of electrons. Each pair of electrons will in general require 2 Hartree products, so as to ensure antisymmetrisation, and, for n electrons, there are n!/2 pairs of electrons. For a three electron system (e.g. the Lithium atom), that means 6 Hartree products, and after a bit of thinking, you can work out that the wavefunction will be of the form:

\[ \Psi(\mbox{x}_1,\mbox{x}_2,\mbox{x}_3)= \left \{ \begin{array}{lll} \chi_1(\mbox{x}_1)\chi_2(\mbox{x}_2)\chi_3(\mbox{x}_3)-\chi_1(\mbox{x}_2)\chi_2(\mbox{x}_1)\chi_3(\mbox{x}_3)+\\ \chi_1(\mbox{x}_2)\chi_2(\mbox{x}_3)\chi_3(\mbox{x}_1)-\chi_1(\mbox{x}_1)\chi_2(\mbox{x}_3)\chi_3(\mbox{x}_2)+\\ \chi_1(\mbox{x}_3)\chi_2(\mbox{x}_1)\chi_3(\mbox{x}_2)-\chi_1(\mbox{x}_3)\chi_2(\mbox{x}_2)\chi_3(\mbox{x}_1) \end{array} \right. \]

Writing out such expressions rapidly becomes tedious; fortunately, they can be written in a completely general way as Determinants (called Slater determinants)

\[ \Psi(\mbox{x}_1,\mbox{x}_2,\mbox{x}_3,\ldots \mbox{x}_n)= \frac{1}{\sqrt{n_{elec}!}} \left | \begin{array}{ccccc} \mathbf{\chi_1(\mbox{x}_1)} & \chi_2(\mbox{x}_1) & \chi_3(\mbox{x}_1) & \cdots & \chi_n(\mbox{x}_1) \\ \chi_1(\mbox{x}_2) & \mathbf{\chi_2(\mbox{x}_2)} & \chi_3(\mbox{x}_2) & \cdots & \chi_n(\mbox{x}_2) \\ \chi_1(\mbox{x}_3) & \chi_2(\mbox{x}_3) & \mathbf{\chi_3(\mbox{x}_3)} & \cdots & \chi_n(\mbox{x}_3) \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \chi_1(\mbox{x}_n) & \chi_2(\mbox{x}_n) & \chi_3(\mbox{x}_n) & \cdots & \mathbf{\chi_n(\mbox{x}_n)} \end{array} \right | \]

In the common situation where there are an even number of electrons in a "closed-shell" situation, they are usually taken to occupy the spatial orbitals two by two, with paired spins: (Here for example with six electrons in three orbitals)

\[ \Psi= \frac{1}{\sqrt{n_{elec}!}} \left | \begin{array}{cccccc} \psi_1(r_1) & \overline{\psi_1(r_1)} & \psi_2(r_1) & \overline{\psi_2(r_1)} & \psi_3(r_1) & \overline{\psi_3(r_1)} \\ \psi_1(r_2) & \overline{\psi_1(r_2)} & \psi_2(r_2) & \overline{\psi_2(r_2)} & \psi_3(r_2) & \overline{\psi_3(r_2)} \\ \psi_1(r_3) & \overline{\psi_1(r_3)} & \psi_2(r_3) & \overline{\psi_2(r_3)} & \psi_3(r_3) & \overline{\psi_3(r_3)} \\ \psi_1(r_4) & \overline{\psi_1(r_4)} & \psi_2(r_4) & \overline{\psi_2(r_4)} & \psi_3(r_4) & \overline{\psi_3(r_4)} \\ \psi_1(r_5) & \overline{\psi_1(r_5)} & \psi_2(r_5) & \overline{\psi_2(r_5)} & \psi_3(r_5) & \overline{\psi_3(r_5)} \\ \psi_1(r_6) & \overline{\psi_1(r_6)} & \psi_2(r_6) & \overline{\psi_2(r_6)} & \psi_3(r_6) & \overline{\psi_3(r_6)} \end{array} \right | \]

This can be written in even shorter form:

\[ \Psi= |\chi_1\chi_2\chi_3\ldots\chi_n \rangle \] \[ \Psi = |\psi_1\overline{\psi_1}\psi_2\overline{\psi_2}\psi_3 \ldots \overline{\psi_n} \rangle \]

Two properties of determinants are important:

  1. The determinant changes sign when two rows (or columns) are exchanged, and therefore
  2. A determinant with two identical rows (or columns) is equal to zero.

From (1), you can check that exchanging the coordinates of any two electrons leads to a change in sign of the whole wavefunction, satisfying the Pauli Principle. From (2), if two electrons occupy the same Spin Orbital, i.e. two columns of the determinant are identical, the wavefunction is equal to zero - which is meaningless, so that such a wavefunction is not acceptable.

Click here to return to the list of online lectures

Click here to return to the previous Section

Click here to go on to the next Section

This page created by Jeremy Harvey, Bristol, 2000.