The Hartree-Fock Method

The Hartree-Fock-Roothaan Method

The Hartree-Fock method involves finding the "best" molecular wavefunction for a given molecular system, using the Molecular Orbital Approximation corrected so as to take the Pauli principle into account.

Energy of a Slater Determinant

As we have seen, molecular orbital wavefunctions need to be written in the form of Slater Determinants so as to satisfy the Pauli Antisymmetry Principle:

$\Psi(\mbox{x}_1,\mbox{x}_2,\mbox{x}_3,\ldots \mbox{x}_n)= \frac{1}{\sqrt{n_{elec}!}} \left | \begin{array}{ccccc} \mathbf{\chi_1(\mbox{x}_1)} & \chi_2(\mbox{x}_1) & \chi_3(\mbox{x}_1) & \cdots & \chi_n(\mbox{x}_1) \\ \chi_1(\mbox{x}_2) & \mathbf{\chi_2(\mbox{x}_2)} & \chi_3(\mbox{x}_2) & \cdots & \chi_n(\mbox{x}_2) \\ \chi_1(\mbox{x}_3) & \chi_2(\mbox{x}_3) & \mathbf{\chi_3(\mbox{x}_3)} & \cdots & \chi_n(\mbox{x}_3) \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \chi_1(\mbox{x}_n) & \chi_2(\mbox{x}_n) & \chi_3(\mbox{x}_n) & \cdots & \mathbf{\chi_n(\mbox{x}_n)} \end{array} \right |$

How does one find the "best" Slater determinant ? By minimising the energy with respect to the coefficients making up the orbitals chi . First, we need to know how to calculate the energy of a Slater Determinant wavefunction. As for any wavefunction, this is done by taking the "average value" of the Hamiltonian over all the space and spin coordinates (x):

$E_{SD}=\int \Psi_{SD}\hat{H}_{elec}\Psi_{SD} d\mbox{x}$

The Hamiltonian operator is given by a sum of n one-electron terms and n(n-1)/2 two-electron terms:

$\hat{H}_{elec}= \sum_{i=1}^{n} \hat{h}_i + \sum_{i}^{n}\sum_{j>i}^{n} \frac{1}{r_{ij}}$

Where the one-electron operators h are given by:

$\hat{h}_i = \frac{-\nabla_i^{2}}{2} + \sum_{A}^{N} \frac{-Z_{A}}{r_{iA}}$

Inserting this into the expression for the energy leads to:

$E_{SD} = \int \Psi \left \{ \sum_{i=1}^{n} \hat{h}_i \right \} \Psi d\mbox{x} + \int \Psi \left \{ \sum_{i}^{n}\sum_{j>i}^{n} \frac{1}{r_{ij}} \right \} \Psi d\mbox{x}$

Both of these terms, which are integrals of sums, can be re-written as sums of integrals as follows:

$E_{SD} = \sum_{i=1}^n \left \{ \int \Psi \hat{h}_i \Psi d\mbox{x}_i \right \} + \sum_i^n\sum_{j>i}^n \left \{ \int \Psi \frac{1}{r_{ij}} \Psi d\mbox{x}_i d\mbox{x}_j \right \}$

Each one-electron operator h only acts on a very small part of the wavefunction, which leads to a considerable simplification of the first term. This term is also very easy to understand: it is a sum of the one-electron energies h_ii of each orbital.

$\sum_{i=1}^{n} \left \{ \int \Psi \hat{h}_i \Psi d\mbox{x}_i \right \} = \sum_{i=1}^{n} \left \{ \int \chi_i \hat{h} \chi_i dr d\omega \right \} = \sum_{i=1}^n h_{ii}$

Note that the one-electron operator h includes a part corresponding to the electron's kinetic energy, and another to the potential energy created by the attractive Coulombic interaction with the nuclei. Therefore, the one-electron energy of an orbital is the sum of a kinetic and a potential part:

$h_{ii}= \left \{ \begin{array}{lll} \displaystyle{\int \chi_i \hat{h} \chi_i dr d\omega} \\ \mbox{ } \\ \displaystyle{\int \chi_i \left ( \frac{-\nabla_i^{2}}{2} + \sum_{A}^{N} \frac{-Z_{A}}{r_{iA}} \right ) \chi_i dr d\omega} \\ \mbox{ } \\ \displaystyle {\int \chi_i \frac{-\nabla_i^{2}}{2} \chi_i dr d\omega + \int \chi_i \left ( \sum_{A}^{N} \frac{-Z_{A}}{r_{iA}} \right ) \chi_i dr d\omega} \\ \mbox{ } \\ t_{e,i} + V_{Ne,i} \end{array} \right.$

The second set of integrals, the two-electron terms, are more complicated, because there are more of them, and because of the antisymmetrisation of the wavefunction !! Each term in the summation looks like:

$\begin{array}{ll} {\displaystyle \iint} \left \{ (\chi_i(\mbox{x}_1)\chi_j(\mbox{x}_2)- \chi_i(\mbox{x}_2)\chi_j(\mbox{x}_1) \right \} {\displaystyle \frac {1}{r_{12}}}\;\;\;\;\; \\ \;\;\;\;\;\;\;\; \left \{ (\chi_i(\mbox{x}_1)\chi_j(\mbox{x}_2)- \chi_i(\mbox{x}_2)\chi_j(\mbox{x}_1) \right \} d\mbox{x}_1d\mbox{x}_2 \end{array}$

This rather daunting expression can be multiplied out, to give four terms:

$\begin{array}{llll} \iint \chi_i(\mbox{x}_1)\chi_j(\mbox{x}_2) {\displaystyle \frac {1}{r_{12}}} \chi_i(\mbox{x}_1)\chi_j(\mbox{x}_2) d\mbox{x}_1d\mbox{x}_2 \\ -\iint \chi_i(\mbox{x}_1)\chi_j(\mbox{x}_2) {\displaystyle \frac {1}{r_{12}}} \chi_i(\mbox{x}_2)\chi_j(\mbox{x}_1) d\mbox{x}_1d\mbox{x}_2 \\ -\iint \chi_i(\mbox{x}_2)\chi_j(\mbox{x}_1) {\displaystyle \frac {1}{r_{12}}} \chi_i(\mbox{x}_1)\chi_j(\mbox{x}_2) d\mbox{x}_1d\mbox{x}_2 \\ \iint \chi_i(\mbox{x}_2)\chi_j(\mbox{x}_1) {\displaystyle \frac {1}{r_{12}}} \chi_i(\mbox{x}_2)\chi_j(\mbox{x}_1) d\mbox{x}_1d\mbox{x}_2 \end{array}$

The first and fourth, and second and third, term are identical two by two. To understand what they both mean, it helps to rewrite them in terms of the spatial orbitals and coordinates (the spin terms are not very important here), and to rearrange them a bit. Taking the first term first (!), it can be written as:

$\iint \psi_i^2(r_1) \frac {1}{r_{12}} \psi_j^2(r_2) dr_1dr_2$

Now, psi ²(r) is the probability of finding an electron at a given point in space. So this first term is simply the energy of the Coulombic interaction between an electron in orbital i with an electron in orbital j. For this reason, this integral is often written as the Coulombic integral, and written in shorthand as J_ij. Because 1/r is always positive, and psi ² obviously also, this term contributes a positive energy, i.e. a destabilisation - this is what you expect from a Coulomb repulsion.

The other integrals become:

$-\iint \psi_i(r_1)\psi_j(r_2) \frac {1}{r_{12}} \psi_i(r_2)\psi_j(r_1) dr_1dr_2$

What does this term, called an Exchange Integral, and written as K_ij, mean ? Unlike for the Coulomb integral, there is no immediate classical interpretation for the Exchange integral. The name Exchange Integral comes from the fact that the two electrons exchange their positions from the left to the right of the integrand. This suggests, correctly, that it has something to do with the Pauli principle.

Remember that the probability density for two electrons is very different in an antisymmetrised Slater Determinant than in a simple Hartree Product. The total density is not simply a sum of the densities associated with each molecular orbital. (See the graphs for the two-electrons-in-a-box model in the section concerning the Pauli Principle.) Yet the expression for the repulsion energy between electrons given by the Coulomb integrals suggests that the total density is a sum of densities - it neglects all the effect of the antisymmetrisation on the density!

However, the expressions we have been deriving are for the energy of a Slater Determinant - so the antisymmetrisation effect should be there, somewhere. In fact it is the the Exchange integrals which "correct" the Coulomb integrals to take into account the antisymmetry of the wavefunction. We saw that the electrons (especially those of same spin) tend to avoid each other rather more in the Slater Determinant model than in the Hartree Product model, so the Coulomb integrals should exagerrate the Coulomb repulsion of the electrons. The Exchange integrals, which are negative, compensate for this exagerration.

(Note that the expression written above for K_ij is not entirely correct. The integral is equal to 0. when the two molecular orbitals involved, chi _i and chi _j, are of opposite spin. In other words, the Coulomb integral on its own gives the correct repulsion between two electrons of opposite spin, but it needs to be corrected by the exchange integral for electrons of same spin.)

Overall, the energy of a Slater Determinant is given by adding up all the terms discussed above. For the general case with matrix elements expressed as spin orbitals, one reaches the following expression:

$E_{SD}=\sum_i^{n_{elec}} h_{ii} + \sum_{i}^{n_{elec}}\sum_{j>i}^{n_{elec}}(J_{ij}-K_{ij})$

A slightly different expression, which is more commonly met in books, is reached if one considers matrix elements over the spatial orbitals, for a closed-shell system (= a spin singlet where all the occupied orbitals have two electrons in them),

$E_{SD}=2\sum_i^{n_{orb}} h_{ii} + \sum_{i}^{n_{orb}}\sum_{j}^{n_{orb}}(2J_{ij}-K_{ij})$

The first term represents the one-electron energy of each electron (its (positive) kinetic energy and (negative, attractive) potential energy with respect to the nuclei), whereas the second represents the Coulombic repulsion between the electrons, expressed as a sum of positive terms (the "Coulombic Integrals"), which give the repulsion between electrons assuming that the two-electron densities are given as a sum of orbital densities, and of negative terms (the "Exchange Integrals"), which give the correction to the Coulomb integrals due to the fact that the wavefunction is antisymmetrised.

When comparing energies of reactants and products, etc., it helps to consider the Total Potential Energy - this is the electronic energy as given above, plus the inter-nuclear repulsion energy:

$V_{tot}(R)=\sum_i^{n_{elec}} h_{ii} + \sum_{i}^{n_{elec}}\sum_{j>i}^{n_{elec}}(J_{ij}-K_{ij})+ \sum_{A}^{N_{nucl}}\sum_{B>A}^{N_{nucl}}\frac{Z_AZ_B}{R_{AB}}$

$V_{tot}(R)=\mbox{T}_e + \mbox{V}_{Ne} + \mbox{V}_{ee} + \mbox{V}_{NN}$

An Example

To get a feel for how all of the above quantities vary upon forming a molecule, let us consider the bonding in the water molecule. We can compare:

The kinetic energy of the electrons (T_e).
The (attractive) potential energy of the electrons in the field of the nuclei (V_Ne).
The one-electron energy (h_1e=T_e+V_Ne).
The total electron-electron repulsion energy (V_ee=J_ee+K_ee).
The total electronic potential energy (V_e=V_Ne+V_ee).
The total electronic energy (E_e=V_e+T_e).
The repulsion between the nuclei (V_NN).
The "Total" energy or "Potential". (V_tot(R)=E_e+V_NN).

(A note on units. Throughout this course, we are implicitly using a set of units called Atomic Units. These are units such that many of the constants involved in the various equations have values of 1.000 and are thus very convenient. The atomic unit of energy is also called a Hartree and is equal to 4.35 10^-18 J - rather small !! - or equivalently to 2625 kJ/mol. The values in the Table below are in kJ/mol).

	H₂O	O	H	O + 2 H	Difference
T_e	198630	195695	1339	198373	257
V_Ne	-519965	-466698	-2647	-471991	-47973
h_1e	-321335	-271003	-1308	-273619	-47716
V_ee	98646	74671	0	74671	23976
V_e	-421318	-392027	-2647	-397321	-23998
E_e	-222689	-196332	-1302	-198948	-23740
V_NN	23105	0	0	0	23105
V_tot	-199583	-196332	-1308	-198948	-635

(To give you a feeling for the order of magnitude of the "Exchange" correction in the interelectronic repulsion term (V_ee), the following values are obtained for water: "Coulombic" Part of the electron-electron repulsion energy (J_ee) = 122060 kJ/mol; "Exchange" Part of the electron-electron repulsion energy (K_ee) = -23413 kJ/mol, total electron-electron repulsion energy (V_ee=J_ee+ K_ee) = 98646 kJ/mol.)

The most important terms are shown on the following picture:

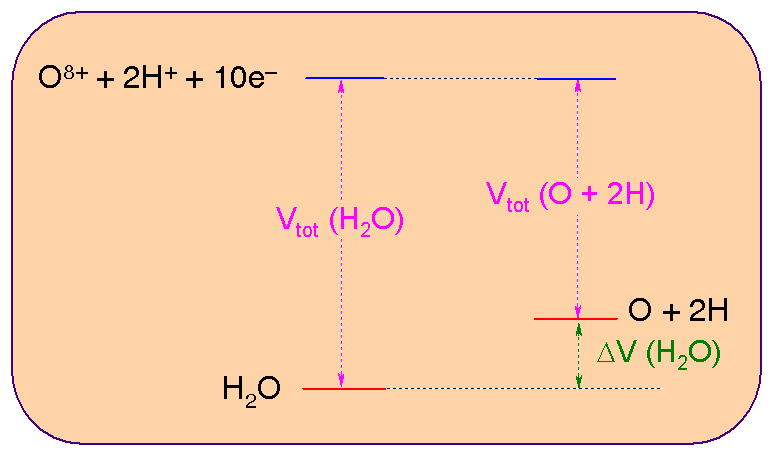
(Note also that the experimental difference in energy is of ca. -930 kJ/mol. The difference between this value and the HF computed number is due to the approximations involved in HF theory).

The Hartree-Fock Roothan Equations

The previous paragraphs show how to calculate the energy of a Slater Determinant. The Hartree-Fock method is then very easy to understand: It simply involves optimizing the spin-orbitals chi to give the lowest energy possible. This is done using a modified version of the Variational Method discussed before for one-electron problems. Like in that case, a differential equation is reduced to a set of homogeneous equations which can be solved using linear algebra. However, some of the details are a bit different, as will be explained below. It may be easier to understand if one first reviews the steps involved in solving a one-particle Schrödinger equation using the Variational Method:

$\mbox{1.} \;\;\;\Psi_j=\sum_i^{n_{basis}}c_{ij}\phi_i \] \[ \mbox{2.} \;\;\;\hat{H}\Psi=E\Psi \] \[ \mbox{3.} \;\;\; \left | \begin{array}{cccc} H_{11}-ES_{11} & H_{12}-ES_{12} & \cdots & H_{1n}-ES_{1n} \\ H_{21}-ES_{21} & H_{22}-ES_{22} & \cdots & H_{2n}-ES_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ H_{n1}-ES_{n1} & H_{n2}-ES_{n2} & \cdots & H_{nn}-ES_{nn} \end{array} \right | = 0 \] \vspace{.5cm} \[ \mbox{4.} \;\;\; \Psi_1= \sum c_{i1}\phi_i \;\; ,\ldots \;\; \Psi_n= \sum c_{in}\phi_i \] \[ \mbox{5.} \;\;\; E_1, E_2, \ldots E_n$

In the Hartree-Fock method, the wavefunction is written as an antisymmetrised product of molecular orbitals, i.e. as a Slater Determinant:

$\mbox{1.} \;\;\; \Psi = \mathcal{A} \prod_i^{n_{el}}\chi_i(\mbox{x}_i)$

This is then inserted in the Schrödinger equation:

$\mbox{2.} \;\;\; \{ \sum_{i=1}^{n} \hat{h}_i + \sum_{i}^{n}\sum_{j>i}^{n} \frac{1}{r_{ij}} \} \Psi=E\Psi$

After substituting (1.) into (2.) and some algebra (...), this equation for 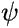Psi can be rewritten as an equation for chi , which is called the Fock Equation:

$\mbox{3.} \;\;\; \hat{\mathcal{F}}\chi=\epsilon\chi$

The Fock Operator 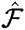$\hat{\mathcal{F}}$ in this equation is a sum of terms corresponding to the one-electron and two-electron terms, h, J and K discussed above.

Unlike the standard variational method, where it is the wavefunction itself which is written as a linear combination of basis functions, here, it is the molecular orbitals which are written as linear combinations of atomic orbitals:

$\mbox{4.} \;\;\;\chi_j=\sum_i^{n_{basis}}c_{ij}\phi_i$

Inserting this expression into the Fock equation, and a bit of algebra, leads to a new set of Secular Equations:

$\mbox{5.} \;\;\;\ \mathbf{FC}-\epsilon\mathbf{SC}=0$

Which can be solved by setting the corresponding Secular Determinant equal to zero:

$\mbox{6.} \;\;\;\ |\mathbf{F}-\epsilon\mathbf{S} |=0$

This yields a set of molecular orbitals, chi _i (given by the coefficients c_ij), with their corresponding "energies" epsilon _i:

$\mbox{7.} \;\;\; \left \{ \begin{array}{ccc} \chi_1 & = & c_{11}\phi_1+c_{21}\phi_2 \cdots + c_{n1}\phi_n \\ \chi_2 & = & c_{12}\phi_1+c_{22}\phi_2 \cdots + c_{n2}\phi_n \\ & \vdots & \\ \chi_n & = & c_{1n}\phi_1+c_{2n}\phi_2 \cdots + c_{nn}\phi_n \end{array}\right. \] \vspace{0.5cm} \[ \mbox{8.} \;\;\; \epsilon_1, \epsilon_2, \ldots \epsilon_n$

The energy of the ground state (for a closed-shell spin-singlet species) is then given by:

$\mbox{9.} \;\;\;E_{HF}=2\sum_i^{n_{orb}}\epsilon_i- \sum_i^{n_{orb}}\sum_j^{n_{orb}}(2J_{ij}-K_{ji}) + \sum_A^{N_{nucl}}\sum_{B>A}^{N_{nucl}} \frac{Z_AZ_B}{R_{AB}}$

There is one further major change with respect to the standard variational method, and that has to do with the nature of the Fock Operator 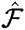$\hat{\mathcal{F}}$ . This is a one-electron operator, that is, it only acts on one molecular orbital. It is given by the following expression (for a closed-shell singlet):

$\hat{\mathcal{F}}=\hat{h}+\sum_j^{n_{orb}}(2\hat{J}_j-\hat{K}_j)$

The Coulomb J_j and Exchange K_j operators have a slighlty peculiar form, which is best understood by looking at what happens when they act on a given molecular orbital (written here as its spatial part):

$\int \psi_i(r_1) \hat{J}_j \psi_i(r_1) \;dr_1 = \iint \psi_i^2(r_1)\frac{1}{r_{12}} \psi_j^2(r_2) \; dr_1dr_2 = J_{ij} \] \[ \int \psi_i(r_1) \hat{K}_j \psi_i(r_1) \;dr_1 = \iint \psi_i(r_1)\psi_j(r_2) \frac{1}{r_{12}}\psi_i(r_2)\psi_j(r_1)\; dr_1dr_2 = K_{ij}$

These operators correspond to the repulsive Coulombic energy between electrons in different molecular orbitals (corrected for the antisymmetrisation "exchange" effect). As can be seen, however, the operator J_j depends on MO number j. This means that the Fock Operator for molecular orbital i depends on the expressions for the all the other molecular orbitals. This means that the procedure (1. - 9.) defined above to get the Hartree-Fock energy and wavefunction of a molecular system is dependent on its own result - so as such, the procedure cannot be followed - it is biting its own tail...

A frankly unnecessary ex cursus: This is reminiscent of the (very popular in mystical circles) imagery of the ouroboros:

To get round this problem, one adopts a so-called Self-Consistent Field procedure. That is, steps 1. - 3. above are followed as normal. The Fock operator is first constructed from a set of guessed MOs 4. (these can be generated in a number of ways, they need to be vaguely similar to the final orbitals, but the details are not important). Then the Fock equation is solved (steps 5. - 7.) to give a new set of orbitals, which will be different from the initially guessed ones. One then loops back to 4., and forms a new Fock operator. This is again used to solve the Fock equation, etc., and so on in a loop until the orbitals cease to change from one step to another. With reasonable guesses and powerful algorithms, 10-20 cycles are usually enough to converge the procedure to numerical accuracy.

Click here to return to the list of online lectures

Click here to return to the previous Section

Click here to go on to the next Section

This page created by Jeremy Harvey, Bristol, 2000.