The Hartree-Fock Method

The Hartree-Fock-Roothaan Method

Applications

What information do we get from the Hartree-Fock method ?

1. Energies

Once the wavefunction has been optimised, we can calculate the total energy of the system, as described in the previous section:

$V_{tot}(R)=E_{\mbox{HF}}+V_{\mbox{nucl}}=\sum_i^{n_{elec}} h_{ii} + \sum_{i}^{n_{elec}}\sum_{j>i}^{n_{elec}}(J_{ij}-K_{ij})+ \sum_{A}^{N_{nucl}}\sum_{B>A}^{N_{nucl}}\frac{Z_AZ_B}{R_{AB}}$

How does this energy relate to the eigenvalues epsilon of the Fock equation? These eigenvalues can be called Orbital Energies, and are given by:

$\epsilon_i = \langle \chi_i | \hat{\mathcal{F}} | \chi_i \rangle = h_{ii} + \sum_j^n(J_{ij}-K_{ij})$

It might seem natural to express the total electronic energy as the sum of the Orbital energies for the occupied orbitals, but this is in fact not so:

$E_{\mbox{HF}} \neq \sum_i^{n_{occ}} \epsilon_i$

This is because the orbital energy includes the interelectronic repulsion - adding the orbital energies up thus counts the repulsion terms twice. The correct energy can be expressed instead as:

$E_{\mbox{HF}} = \sum_i^{n_{elec}} \epsilon_i - \sum_{i}^{n_{elec}}\sum_{j>i}^{n_{elec}}(J_{ij}-K_{ij})$

Remember, Hartree-Fock theory relies on the validity of the Molecular Orbital Approximation. In fact, wavefunctions are more complicated than single Slater Determinants, so that within the Variational procedure, the Hartree-Fock total energy will inevitably be higher than the true energy. However, the difference is very small !!! Hartree-Fock theory is an incredibly good approximation in many ways !!

Some examples:

Species	V_tot (est.)	V_tot (HF)
H₂	-3076	-2973
H₂O	-200306	-199576
Benzene	-608203	-605471
CCl₃H	-2513856	-2512452

Consider a species M described by the Hartree-Fock wavefunction 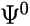$\Psi^0$ . What is the energy of the Slater Determinant obtained by removing an electron from occupied orbital a ?

$E(\Psi^a) = \sum_{i \neq a}^{n_{elec}} h_{ii} + \sum_{i \neq a}^{n_{elec}}\sum_{j>i, \neq a}^{n_{elec}}(J_{ij}-K_{ij}) \] \[ E(\Psi^0) = \sum_i^{n_{elec}} h_{ii} + \sum_{i}^{n_{elec}}\sum_{j>i}^{n_{elec}}(J_{ij}-K_{ij}) \] \[ \mbox{IE(M)} \approx \left ( E(\Psi^a) - E(\Psi^0) \right ) = -h_{aa} -\sum_j(J_{aj}-K_{aj})= -\epsilon_a$

This result is known as Koopmans' Theorem and provides a useful first approximation to molecular ionisation energies.

Species	IE(exp,kJ/mol)	-(HOMO)
H₂	1490	1570
NH₃	970	1098
Benzene	890	870
Toluene	850	835

2. Molecular Orbitals

The molecular orbitals are found from solving the Fock equation. For a closed-shell spin-singlet with n_elec electrons, the n_elec / 2 orbitals with lowest energy are occupied, each by two electrons. The highest occupied orbital (HOMO) and the lowest unoccupied one (LUMO) are useful for understanding reactivity.

3. A Wavefunction

This is written as a Slater Determinant: (here in brief form)

$\Psi= |\chi_1\chi_2\chi_3\ldots\chi_n \rangle$

A wavefunction allows you to calculate a huge number of properties of a system. In technical terms, this is because to each property, there is an associated Operator, and the observed value of the property is simply the value of that operator, averaged over the wavefunction (expectation value of the wavefunction:

$\mbox{P}_{\mbox{obs.}} = \langle \Psi | \mathcal{O}(P) | \Psi \rangle$

Some examples are given below.

4. Dipole Moments

The dipole moment of a set of charged particles is given by the product of the difference between the total positive and negative charges, and the distance between the average centre-of-charge positions of the two charge clouds. This is computed very easily from a wavefunction:

$\vec{\mu} = \langle \Psi | -\vec{r}_i | \Psi \rangle + \sum_A Z_a\vec{R}_A$

This is the dipole associated with a molecule of fluoromethane:

The underlying reason for the dipole is that the C-F sigma bond is polarised towards Fluorine. With some will-power, this can be seen on a plot of the corresponding MO:

Calculating dipoles is so easy that programs which perform Hartree-Fock computations will always provide you with the dipole (and the quadrupole, octapole, hexadecapole, etc.).

Atomic Charges

The atomic charges shown above on C and F can also be derived from the wavefunction. Basically, one takes the total electron density, and finds some way to split it up into parts "belonging" to the individual atoms. It turns out that there is no theoretically "best" way to do the splitting up. One popular procedure was suggested by Mulliken, and is called Mulliken Population Analysis. This often provides useful trends but also often produces meaningless results !

5. Electrostatic Potential

With a wavefunction, it is also easy to calculate the Electrostatic Potential at each point in space. This is the energy required to bring a (hypothetical) point charge from infinity. It provides useful three- dimensional insight into the polarity of a molecule.

This picture shows the Electrostatic Potential around the fluoromethane molecule (plotted onto an isodensity surface of the electron density. The reddest regions are most attractive to negatively-charged species, and the blue-est ones to positively charged ones). The electron attracting region in the centre of the methyl group can be related (with slightly less need for the eyes of faith) to the structure of the LUMO:

Such plots of the electrostatic potential are often used by theoretical chemists working in biochemistry or pharamceutical chemistry - the polarity of molecules strongly relates to how they interact with enzymes. As a (slightly) more relevant example of this, here is an Electrostatic Potential plot for the amino acid Valine, in its zwitterionic form (H₃C)₂CH- CH(NH₃⁺)(CO₂^-):

6. Geometries

Up till now, we have considered solving the Schrödinger equation for a fixed position of the nuclei. As discussed in the first section, the electronic energy (or equivalently the Potential) is a Function of the positions of the nuclei.

$V_{tot}(R)= \langle \Psi_{elec}(R) | \hat{H}_{elec} | \Psi_{elec}(R) \rangle + \sum_{A}^{N_{nucl}}\sum_{B>A}^{N_{nucl}}\frac{Z_AZ_B}{R_{AB}}$

This defines a so-called Potential Energy Surface. Stable structures of molecules correspond to R coordinates such that V(R) is low. For example, if one solves the Schrödinger equation for the hydrogen molecule at a set of internuclear distances, one obtains the following graph:

For larger molecules, it is useful to recognise that the expression shown above is a Function of the coordinates R. Like all functions, it can be differentiated. This leads to the Gradient of the Potential Energy:

$\vec{G}(R)= \frac{\partial \left \{ \langle \Psi(R) | \hat{H}(R) | \Psi(R) \rangle + \sum_{A,B} Z_AZ_B/R_{AB} \right \} } {\partial R}$

Calculating this derivative is not easy, but the necessary equations have been worked out, and the corresponding computation carried out once the wavefunction is known. Knowing the slope of the surface enables one to use advanced mathematical optimisation techniques so as to find optimum geometries (where the gradient is equal to zero). In this way, stable molecular structures for large molecules can be determined.

Carbene

The carbene (or methylene) intermediate, CH₂ is an unstable intermediate involved in several organic reactions. Its gas-phase structure was long uncertain. In 1959, Foster and Boys predicted it to be bent on the basis of ab initio calculations, with an H-C-H angle of 129 degrees. The first experimental report was by the eminent physical chemist Gerhard Herzberg, in 1961, who analyzed the electronic spectrum and predicted the molecule to have a linear structure. In those times, computational predictions were not taken very seriously, so doubt was laid on the reliability of the calculations. In 1970, new and thorough HF calculations by Bender and Schaeffer lead to the conclusion that carbene is bent. This was followed in the next years by new experiments which found carbene to be... bent !

Nowadays, computational methods are routinely used to predict molecular geometries, with an accuracy which is similar or better to that of most experimental methods.

Chemical Reactivity

The study of potential energy surfaces also provides insight into chemical reactivity. The key here is to find Transition States, or saddle-points, the lowest energy cols which need to be crossed on going from one valley to another:

Locating transition states gives useful information on Reaction Mechanisms, as well as on Activation Energies and Reaction Rates, combined e.g. with Transition State Theory.

7. Other Properties

Many other properties can be computed: NMR chemical shift, NMR spin coupling constants, IR spectra, UV spectra, ... Some of these are easy to compute - some less so.

Applicability of Hartree-Fock Theory

How easy is it to perform a Hartree-Fock calculation?

Some 50 years ago, the answer would have been "Not at all". Performing Hartree-Fock calculations on paper for anything but the very simplest of systems is rapidly rather tiresome... Since then, computers have made their appearance and a standard PC is now more powerful than essentially all computers were 20 years ago, and than many computers 10 years ago. General software packages for performing Hartree-Fock and other ab initio computations have been developed which make it unnecessary to delve into the murky depths of the maths. Molecules can be "built" on the screen by clicking atoms into place.

How long do calculations take ? The bigger the molecule, the longer. In formal terms, the most time-consuming operation is the need to calculate all of the following "two-electron" integrals over the basis functions:

$(ab|cd) = \iint \phi_a(r_1)\phi_b(r_1)\frac{1}{r_{12}}\phi_c(r_2)\phi_d(r_2) \; dr_1dr_2$

There are roughly N⁴/8 integrals of this form, where N is the number of basis functions. As a crude estimate, each atom needs of the order of 10 basis functions to be well described. For 2 atoms, there are therefore roughly 20000 integrals. For 10 atoms, there are 12753775... This is shown on the following graph:

This poor scaling has historically made ab initio calculations difficult for large molecules. However, new, more efficient algorithms which e.g. manage to avoid calculating all of the two-electron integrals, together with ever more powerful computers mean that computations are now possible on MUCH larger molecules than before. As an example, a HF calculation with geometry optimisation was recently reported for the (rather small, only 650 atoms) protein, Crambin:

(If you have the Chime plug-in, you can click on the image to view it in 3 dimensions.)

The increasing applicability of ab initio theory means that many research papers nowadays include computational studies using the methods of electronic structure.

The development of efficient ab initio software such as Gaussian, GAMESS, MOLPRO, MOLCAS, CadPac, Jaguar, ADF, Turbomole, etc., has been carried out by a large number of research groups, with British scientists among others playing a leading role. To single out one name among many others, John Pople, who was awarded the Nobel prize in 1998 for his work in the field, has done more than anyone else to make the methods more efficient and to make their application more popular among research chemists.

Click here to return to the list of online lectures

Click here to return to the previous Section

Click here to go on to the next Section

This page created by Jeremy Harvey, Bristol, 2000.