Uvažujme dutú sféru s polomerom R,
ktorá nesie na povrchu elektrický náboj s plošnou hustotou s.
Situáciu znázorňuje obr. 6.1.9.3 Dutosť telesa (gule) predpokladáme z toho dôvodu,
aby sme sa vyhli vzájomnému pôsobeniu náboja na povrchu gule s nábojmi v látke,
z ktorej je teleso. Je to zložitý
problém, ktorému sa budeme venovať až v ďalšej kapitole.
Budeme postupovať podobne ako v predchádzajúcom prípade. Stred
súradnicovej sústavy umiestnime do stredu gule. Pre úlohu je typická sférická
symetria, z čoho vyplýva radiálny smer vektora E.
Jeho veľkosť E je potom funkciou iba
vzdialenosti r od stredu.
Plochu S budeme voliť ako
sférickú plochu o polomere r. Na
tejto sférickej ploche je potom vektor E vždy rovnobežný s miestnou normálou n a pre tok elektrostatického poľa dostaneme
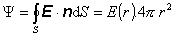 (6.1.55)
(6.1.55)
Teraz musíme rozlišovať dva prípady r
< R a r > R. Ak r < R, tak vo vnútri gule nie je žiaden elektrický náboj, a preto tok Y = 0. Z toho ihneď vyplýva
E = 0 , ak r < R (6.1.56)
|
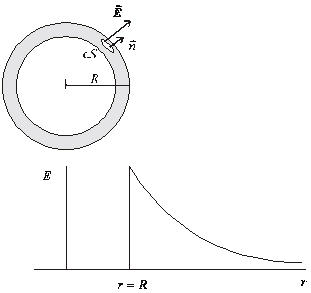
Obr.
6.1.9.3
|
V druhom prípade, ak r > R, tak vo vnútri plochy S sa nachádza všetok náboj, ktorý je na
povrchu nabitej gule, takže podľa Gaussovej vety platí
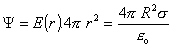 (6.1.57)
(6.1.57)
z čoho vyplýva
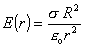 , ak r
> R (6.1.58)
, ak r
> R (6.1.58)
Závislosť
intenzity poľa od vzdialenosti r od stredu gule je znázornená na obr. 6.1.9.3.
Na funkčnej závislosti E(r) nás prekvapuje nespojitosť v bode r = R.
Tu si znova musíme pripomenúť, že sme
pracovali s abstrakciou gule, kde sa náboj na povrchu rozkladá v nekonečne
tenkej vrstve. V skutočnosti, ak máme teleso nabité na povrchu, tak tento
elektrický náboj sa vždy rozprestiera vo vrstve konečnej hrúbky. Výpočty
ukazujú, že napríklad v kovoch hrúbka takejto vrstvy predstavuje niekoľkých
atomárnych rovín, čo je však z makroskopického hľadiska zanedbateľná
hrúbka. V rozsahu takejto veľmi tenkej vrstvy potom elektrické pole spojito
narastá z nuly na konečnú hodnotu tesne nad povrchom ( E(R) = s / eo)