Máme guľu (sféru) s polomerom R,
ktorá je rovnomerne nabitá elektrickým nábojom s objemovou hustotou r.
Situáciu znázorňuje obr. 6.1.17. Pre
tento prípad je typická sférická symetria úlohy, t.j. že pri otočení systému
okolo ľubovoľnej osi prechádzajúcej stredom gule sa žiadna fyzikálna veličina
nemení. Z toho vyplýva, že:
·
elektrické pole má radiálny smer
·
veľkosť vektora E t.j. E = |E | je funkciou iba vzdialenosti r
od stredu gule.
|
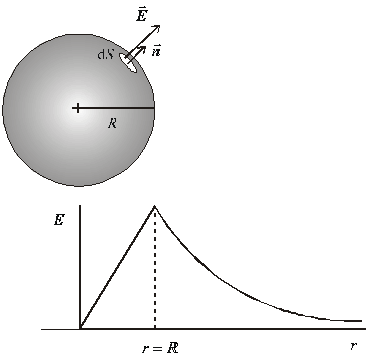
Obr.
6.1.9.2 Výpočet elektrického poľa rovnomerne nabitej gule.
|
V tomto prípade je
najvýhodnejšie zvoliť plochu S ako
sférickú plochu o polomere r. Potom
pole E na povrchu plochy je v každom
bode rovnobežné s normálou n k ploche
S. Tok elektrického poľa potom ľahko
dostaneme
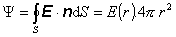 (6.1.49)
(6.1.49)
Náboj q, ktorý je takouto plochou obklopený
závisí od polomeru r. Ak je r < R, tak vo vnútri plochy sa nachádza iba časť náboja celého telesa
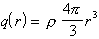 (6.1.50)
(6.1.50)
Z Gaussovej vety potom vyplýva
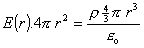 (56.1.1)
(56.1.1)
z čoho po úprave dostaneme
 pre r < R (6.1.52)
pre r < R (6.1.52)
Pre plochy S, kde r > R je náboj vo vnútri plochy konštantný
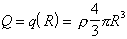 , (6.1.53)
, (6.1.53)
takže pre výsledné pole
dostaneme
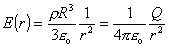 r > R (6.1.54)
r > R (6.1.54)
Priebeh
veľkosti vektora intenzity poľa E je
znázornený na obr. 6.1.9.2. Vidíme, že veľkosť vektora od stredu gule najprv
lineárne vzrastá. Najväčšiu hodnotu dosahuje na povrchu gule. Elektrické pole
mimo nabitej gule klesá so štvorcom vzdialenosti. Výsledok je dôležitý aj z
toho hľadiska, že pole rovnomerne nabitej gule v priestore mimo nej je presne
také isté ako pole bodového náboja umiestneného v jej strede, rovnakej
veľkosti ako je celkový náboj gule. Toto do istej miery oprávňuje aproximáciu
nabitých telies bodovými nábojmi.