Predstavme si
dlhé tenké vlákno, ktoré je elektricky nabité s konštantnou dĺžkovou hustotou l. Pozri
obrázok 9. Za-veďme si súradnicovú
sústavu x, y, z tak, že os y je spojená s vláknom a os x pre-chádza bodom pozorovania P, ktorý
je vo vzdialenosti a od nabitého vlákna.
Element vlákna v bode A(0, y) s
dĺžkou dy generuje príspevok dE k výslednému elektrickému poľu E.
Ku každému takémuto elementu však v bode B(0,-y) existuje element dy´,
ktorý generuje príspevok dE´, taký,
že y-ové zložky vektorov dE a dE´sa vyrušia. Preto nám ďalej stačí počítať iba x-ové zložky jednotlivých vektorov.
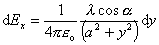(6.1.24)
Keďže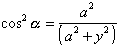 
, tak dostaneme
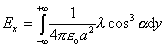(6.1.25)
V tomto prípade sa pokúsime
vypočítať integrál trigonometrickou substitúciou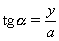 
Pričom
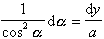
Po dosadení dostávame
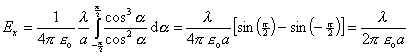
Teda
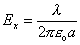(6.1.26)
Výsledok, ktorý sme dostali, je
zaujímavý z toho hľadiska, že výsledný vektor poľa je kolmý na nabité vlákno
a jeho veľkosť klesá s prvou mocninou vzdialenosti do vlákna.
Samozrejme, nekonečne dlhé nabité vlákno je iba abstrakcia. V skutočnosti
existujú iba nabité vlákna konečnej dĺžky. V takom prípade vzťah (6.1.26) platí iba v tesnej blízkosti
vlákna. Vo vzdialenostiach oveľa väčších ako je dĺžka vlákna bude pole závisieť
od celkového náboja na vlákne a klesať so štvorcom vzdialenosti.
