Na obr. 8 je
znázornená kruhová doska, ktorá je rovnomerne pokrytá nábojom s plošnou
hustotou s. (Môžeme si predstaviť, že náboj sa nachádza na každej strane dosky s
polovičnou hustotou).
Vyberme si na
doske malý plošný element dS vo
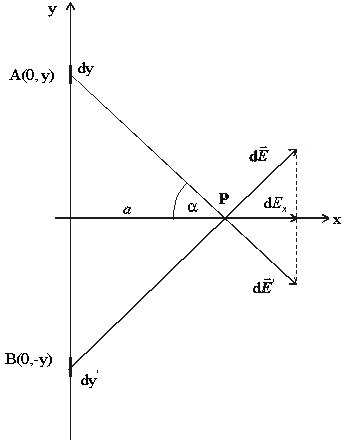
vzdialenosti r od stredu dosky. Na obrázku je znázornený príspevok dE k celkovej intenzite E na osi vo vzdialenosti a od stredu. Z kruhovej symetrie dosky je zrejmé ( a preto počítame pole iba na osi dosky),
že ku každému elementu dS existuje na
protiľahlej strane dosky rovnako veľký element dS´, ktorého príspevok dE´ bude
zrkadlovým obrazom príspevku dE vzhľadom
na rovinu, ktorá prechádza osou dosky a je kolmá na obrázok. Z obrázku je
zrejmé, že u každej takejto dvojice elementov sa zložky kolmé na os (z) dosky vyrušia a príspevky rovnobežné s osou dosky sa algebraicky
sčítajú. To znamená, že ďalej nám stačí počítať iba príspevky k poľu iba v
tomto jedinom smere.
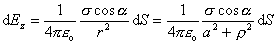 (6.1.17)
(6.1.17)
Všetky
náboje, ktoré sa nachádzajú vo vzdialenosti r od stredu dosky dávajú rovnaký príspevok dEz. Preto môžeme plošný element dS voliť ako medzikružie s polomerom r
a hrúbke dr. Potom
|
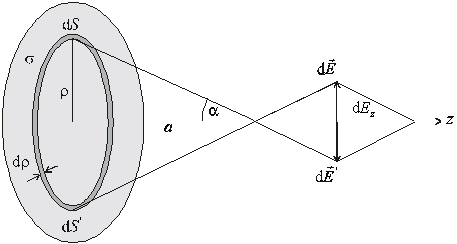
Obr. 6.1.6.1
Elektrostatické pole na osi rovnomerne nabitej
dosky
|
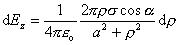 (6.1.18)
(6.1.18)
Výsledná
intenzita má jedinú nenulovú zložku v smere osi z, čiže
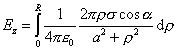 (6.1.19)
(6.1.19)
Keďže 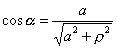 , tak
, tak
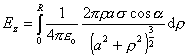 (6.1.20)
(6.1.20)
Zavedením
substitúcie t = (a2 + r2) , ( dt
= 2rdr)
dostaneme
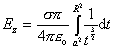 (6.1.21)
(6.1.21)
kde sme konštantné veličiny
vyňali pred integrál. Integrovanie sa týka jednoduchej mocninnej funkcie, takže
pre výsledné pole dostaneme
|
Obr.6.1.6.2
|
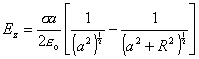 =
= 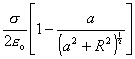 (6.1.22)
(6.1.22)
Výsledok ku
ktorému sme dospeli má však iba obmedzenú platnosť pre os dosky. Zaujímavý je
však limitný prípad, keď bod pozorovania je tesne nad stredom dosky a/R -> 0
a vtedy dostávame
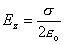 (6.1.23)
(6.1.23)
Tento
výsledok môžeme interpretovať aj inakšie, a to tak, že budeme považovať
vzdialenosť a za konečnú, ale polomer
dosky R budeme neobmedzene zväčšovať.
Tým sa dostávame k abstrakcii nekonečnej nabitej roviny, pre ktorú je každá
priamka kolmá na rovinu jej osou. Pripomíname, že ide o idealizáciu, v praxi sa
môžu vyskytovať nabité roviny iba konečných rozmerov.