- 1.
- Ukážte, že vlna
| 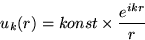 |
(1) |
je sféricky symetrické riešenie vlnovej rovnice.
Konštantu určte tak, aby podľa Huygensovho princípu
príspevok od nekonečnej roviny vĺn s rovnakou fázou
dal spolu rovinnú vlnu.( 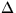 v sférických
súradniciach, pre symetrický problém, t.j.
v sférických
súradniciach, pre symetrický problém, t.j.
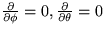 , je
, je 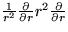 . Použite
paraxiálnu aproximáciu, kde
. Použite
paraxiálnu aproximáciu, kde 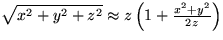 pre
nekonečnú rovinu z=0. )
pre
nekonečnú rovinu z=0. )
[ 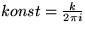 ]
]
- 2.
- Uvažujte kruhovú štrbinu s polomerom r0. Ako sa
závisí intenzina
vlnenia na osi prechádzajúcej otvorom
od vzdialenosti od otvora ( v rámci paraxiálnej approx.)?
Nakreslite obrázok. ( Frenelove zóny. )
[ 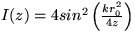 ]
]
- 3.
- Pomocou Huygensovho princípu
spočítajte difrakčný obrazec od nekonečne dlhej,
štrbiny s šírkou a na tienidle vo vzdialenosti
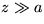 . Uvážte pritom, že pre veľkú
vzdialneosť obrazcu od štrbiny je
. Uvážte pritom, že pre veľkú
vzdialneosť obrazcu od štrbiny je 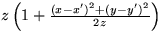
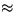
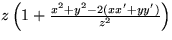 .
. [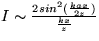 ]
]
- 4.
- Prečo je kov v oblasti viditeľného svetla
silne reflektívny? Zdôvodnite kvantitatívnym
odhadom (
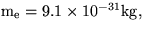
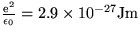 ,
, 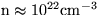 ,
, 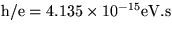 ).
Skúste pouvažovať nad modelom absolútne čierneho
telesa zostaveného z dutej kocky z tenkými kovovými stenami.
Nakoľko môže hrúbka týchto stien ovplyvniť
takýto model? (Skin efekt).
).
Skúste pouvažovať nad modelom absolútne čierneho
telesa zostaveného z dutej kocky z tenkými kovovými stenami.
Nakoľko môže hrúbka týchto stien ovplyvniť
takýto model? (Skin efekt).
[ Nájdite dielektrickú funkciu
elektrónového plynu 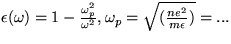 a riešte el.mag. pole v takomto prostredí.]
a riešte el.mag. pole v takomto prostredí.]
- 5.
- Na Zem prichádza slnečné žiarenie s plošnou
hustotou výkonu P = 700 W/m2. Aká je teplota na Slnku?
( Polomer Slnka R0=600000 km, vzdialenosť Zem - Slnko je
150 miliónov km,
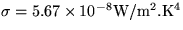 .)
.)
[ 6000 K. ]
- 6.
- Maximum intenzity vyžarovania wolframového vlákna
pripadá na
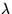 = 966 nm. Priemer vlákna d = 0.2 mm,
dĺžka l=1cm. Za aký čas poklesne teplota na izbovú
po jej vypnutí? (
= 966 nm. Priemer vlákna d = 0.2 mm,
dĺžka l=1cm. Za aký čas poklesne teplota na izbovú
po jej vypnutí? ( 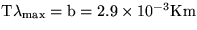 ,
, 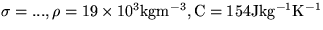 .)
.)
![$[ t = \frac{d \rho C}{12 \sigma} \left( \frac{1}{T_{0}^{3}} -
\frac{\lambda^{3}}{b^{3}} \right) \approx 34 s .]$](img22.gif)
- 7.
- Wolfrámová žiarovka je kov a nie hypotetické
čierne teleso. Za akých podmienok možno
použiť model absolúlne čierneho telesa aj v
tomto prípade (Skin efekt + hrúbka vlákna)?
Pre popis kovu uvažujte dielektrickú konštantu
odvodenú v príklade "kov ako zrkadlo".
- 8.
- Bude platiť analóg Wienovho zákona aj pre
rozpálenú železnú tehlu? Uvážte, že
pre elmag. vlny v kove platí disperzný vzťah
| 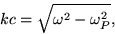 |
(2) |
kde c je rýchlosť svetla vo vákuu, k
veľkosť vlnového vektora, 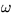 uhlová
frekvencia elmag. vlny a
uhlová
frekvencia elmag. vlny a 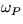 plazmová
frekvencia kovu (viď. príklad "kov ako zrkadlo").
plazmová
frekvencia kovu (viď. príklad "kov ako zrkadlo").
[ Áno. ]
- 9.
- Prečo voľný elektrón nedokáže
absorbovať fotón?
[ ZZE a ZZH nedajú fyzikálne riešenie -
ukázať. ]
- 10.
- Atóm v pokoji prechádza zo stavu s energiou W1 do
stavu s energiou W1 a vyžiari pritom fotón
s energiou
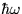 . Ak sa ten istý atóm pohybuje
v smere osi z rýchlosťou v1 a vyžiari pri
tom istom prechode fotón pod uhlom
. Ak sa ten istý atóm pohybuje
v smere osi z rýchlosťou v1 a vyžiari pri
tom istom prechode fotón pod uhlom 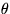 s osou z. Aká
je energia takéhoto fotónu, a ako súvisí s
Dopplerovým efektom?
s osou z. Aká
je energia takéhoto fotónu, a ako súvisí s
Dopplerovým efektom?
![$[ \hbar \omega ' = \frac{ \hbar \omega }{ 1 - \frac{v_{1}}{c}
\cos{(\theta)} } .]$](img28.gif)
- 11.
- Ukážte, že pohybu častice zodpovedá grupová
rýchlosť
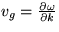 a nie fázová rýchlosť
a nie fázová rýchlosť 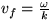 . Uvažujte jedno-rozmerný vlnový balík
. Uvažujte jedno-rozmerný vlnový balík
| 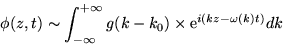 |
(3) |
kde k0 je klnový vektor dávajúci
najvýraznejší príspevok ku sume týchto
rovinných vĺn (g(k-k0) má výrazné maximum
pre k=k0). V takomto prípade 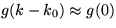 pre
pre
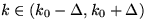 a pre iné k je celý
integrál efektívne nulový. V intervale
a pre iné k je celý
integrál efektívne nulový. V intervale
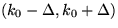 možno
možno 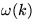 rozvinúť
do taylorovho radu
rozvinúť
do taylorovho radu 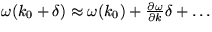 . Po
uvážení týchto faktov je integrál (
. Po
uvážení týchto faktov je integrál (![[*]](/pics/cross_ref_motif.gif) )
vyčísliteľný. Pohyb častice zrejme zodpovedá
pohybu maxima tohto balíka.
)
vyčísliteľný. Pohyb častice zrejme zodpovedá
pohybu maxima tohto balíka.
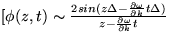 , čo má polohu maxima
danú
, čo má polohu maxima
danú ![$z_{max} = \frac{\partial \omega}{\partial k} t ]$](img38.gif) .
.
- 12.
- Rovnice elektromagnetizmu sú relativisticky korektné,
nakoľko správne opisujú el.mag. pole, aj keď sa
fotóny pohybujú rýchlosťou v = c (vo vákuu).
Správna (relativisticky invariantná, t.j. je rovnaká
v čiarkovanej aj v nečiarkovanej sústave) je teda aj
vlnová rovnica
| 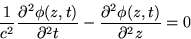 |
(4) |
Uvažujte ľubovoľnú lineárnu transformáciu
súradníc a času
|  |
(5) |
s podmienkou, že počiatok čiarkovanej sústavy
sa pohybuje vzhľadom na nečiarkovanú rýchlosťou
u (t.j. u = a12/a11, prečo?). Aké podmienky
vyplývajú z invariancie rovnice (![[*]](/pics/cross_ref_motif.gif) ) na koeficienty
aij?
) na koeficienty
aij?
[Transformácia (![[*]](/pics/cross_ref_motif.gif) ) je špeciálna
Lorentzova transformácia. Inač povedané, vlnová
rovnica s fázovou rýchlosťou vf=c je relativisticky
invariantná.]
) je špeciálna
Lorentzova transformácia. Inač povedané, vlnová
rovnica s fázovou rýchlosťou vf=c je relativisticky
invariantná.]
- 13.
- Na základe invariancie vlnovej rovnice (
![[*]](/pics/cross_ref_motif.gif) ) nájdite
relativistický vzťah pre Dopplerov effekt. Pomôcka:
Musí zrejme platiť
) nájdite
relativistický vzťah pre Dopplerov effekt. Pomôcka:
Musí zrejme platiť 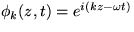 =
=
 , kde
, kde 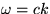 a
a
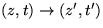 podľa špeciálnej
Lorentzovej transformácie.
podľa špeciálnej
Lorentzovej transformácie.
[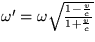 , kde
, kde 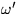 je frekvencia v pohybujúcej sa sústave.]
je frekvencia v pohybujúcej sa sústave.]
- 14.
- Pióny
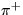 a
a 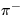 sú nestabilné - rozpadajú
sa s polčasom
sú nestabilné - rozpadajú
sa s polčasom 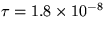 s. Akú dráhu
ubehnú v laboratóriu, keď sa ich polovica rozpadne ak
sa šíria rýchlosťou v=0.996 c ?
s. Akú dráhu
ubehnú v laboratóriu, keď sa ich polovica rozpadne ak
sa šíria rýchlosťou v=0.996 c ?
[ Klasicky s = 5.38 m; relativisticky s = 60m. ]
- 15.
- Intenzita elektrickáho poľa je E = 109V/m.
Nájdite všeobecný vzťah pre rýchlosť (v(t)) a
prejdenú dráhu (x(t)) elektrónu vzhľadom na
sústavu v pokoji, ako aj jeho
vlastný čas (
 ) zodpovedajúci času t v
pokojovej sústave. Aké je zrýchlenie elektrónu a
jeho kinetická energia v okamihu, keď v = 108m/s?
) zodpovedajúci času t v
pokojovej sústave. Aké je zrýchlenie elektrónu a
jeho kinetická energia v okamihu, keď v = 108m/s?
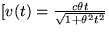 ,
, 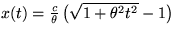 ,
, 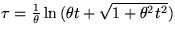 ,
kde
,
kde 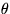 = eE/m0c,
= eE/m0c, ![$
\frac{d v}{d t} = \frac{eE}{m_{0}}\left( 1 -
\frac{v^{2}}{c^{2}} \right)^{3/2} = 1.5 \times 10^{20} ms^{-2}. ] $](img54.gif)
- 16.
- Odhadnite energiu elektrónu v atóme vodíka
pomocou princípu neurčitosti.
Pre strednú energiu platí 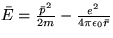 , pričom pre základný stav
, pričom pre základný stav 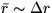 a
podobne
a
podobne 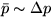 . Uvážením
. Uvážením
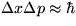 , má
, má 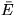 minimum
pre
minimum
pre 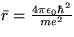 . To dáva 'prekvapivo' dobrý výsledok
. To dáva 'prekvapivo' dobrý výsledok
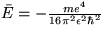 .
.
- 17.
- Na najjednoduchšom prípade kvantovej sústavy -
častici v nekonečne hlbokej potenciálovej jame -
si precvičte 1. hľadanie úplného systému
vlastných stavov, 2. normovanie vlnových funkcií,
3. počítanie stredných hodnôt operátorov,
4. nájdite neurčitosť hybnosti a polohy v
najnižšom a prvom excitovanom stave, overte princíp
neurčitosti, 5. použitím symetrickej geometrie pre
jamu (V(x)=0 pre x
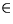 (-a/2,a/2), ináč V(x) = +
(-a/2,a/2), ináč V(x) = +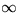 ) posúďte symetriu vlnových funkcií, 6. aký bude
časový vývoj pravdepodobnosti nachádzania sa častice
na mieste x v čase t, ak počiatočný stav je
daný lin.kombináciou základného a prvého
vzbudeného stavu?
) posúďte symetriu vlnových funkcií, 6. aký bude
časový vývoj pravdepodobnosti nachádzania sa častice
na mieste x v čase t, ak počiatočný stav je
daný lin.kombináciou základného a prvého
vzbudeného stavu?
Všetko okrem 6. je v každom úvodnom texte
ku kvantovej mechanike, napr. Krempaský Fyzika,
Pišút, Černý, Gomolčák Úvod
do kvantovej mechaniky. 6. Keďže H(x) = H(-x), potom
( H(x) 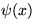 = E
= E 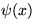 ) = (zámena x -> -x) ( H(-x)
) = (zámena x -> -x) ( H(-x)
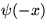 = E
= E 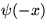 ) = (symetria H(x)) ( H(x)
) = (symetria H(x)) ( H(x) 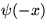 =
E
=
E 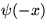 ).
Posledná rovnosť znamená, že
).
Posledná rovnosť znamená, že 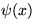 a
a 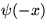 majú rovnakú vlastnú energiu, t.j.
majú rovnakú vlastnú energiu, t.j. 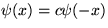 .
Pretože
.
Pretože 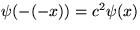 dostávame
c =
dostávame
c = 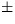 1. To znamená, že každá vlastná
funkcia H je buď párna alebo nepárna.
1. To znamená, že každá vlastná
funkcia H je buď párna alebo nepárna.
- 18.
- Riešte potenciálovú jamu s konečnou hĺbkou.
Aké podmienky musí spĺnať vlonová funkcia
z bode, kde je potenciálna energia V(x) nespojitá?
Pre hľadaní riešenia využite znalosť symetrie
hamiltoniánu. Nájdite počet viazaných stavov na
jame s potenciálom V(x) = -Vo pre x
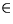 (-a/2,a/2). Pre
akú
šírku a potenciál existuje iba jeden viazaný stav?
Zdôvodnite opodstatnenosť nulových okrajových
podmienok pre nekonečne hlbokú jamu.
(-a/2,a/2). Pre
akú
šírku a potenciál existuje iba jeden viazaný stav?
Zdôvodnite opodstatnenosť nulových okrajových
podmienok pre nekonečne hlbokú jamu.
Opäť štandardný príklad z
štandardných učebníc.
- 19.
- Riešte rozptyl volnej častice na bariére s potenciálom
V(x), kde V(x) = Vo > 0 pre
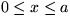 a
V(x)=0 inde, t.j. príslušnú Schrödingerovu rovnicu s
okrajovou podmienkou
a
V(x)=0 inde, t.j. príslušnú Schrödingerovu rovnicu s
okrajovou podmienkou 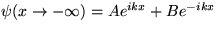 a
a 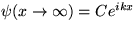 (viď
obr.(
(viď
obr.(![[*]](/pics/cross_ref_motif.gif) )). Vlna s A
reprezentuje dopadajúcu časť vlnovej funkie, B
odrazenú a C prechádzajúcu. Pre aké energie
(vlnové
dĺžky) nedochádza ku odrazu? Pre aké energie
dochádza ku rezonancii, t.j. pre nekonečne malú
amplitúdu dopadajúcej vlny A je C aj B konečne
veľké? Ako je situácia závislá od rozdielu
energii voľnej častici E a potenciálom Vo?
Ako sa zmení situácia, pre Vo < 0 a ako to súvisí
z lokalizovanými stavmi na takejto potenciálovej jame?
)). Vlna s A
reprezentuje dopadajúcu časť vlnovej funkie, B
odrazenú a C prechádzajúcu. Pre aké energie
(vlnové
dĺžky) nedochádza ku odrazu? Pre aké energie
dochádza ku rezonancii, t.j. pre nekonečne malú
amplitúdu dopadajúcej vlny A je C aj B konečne
veľké? Ako je situácia závislá od rozdielu
energii voľnej častici E a potenciálom Vo?
Ako sa zmení situácia, pre Vo < 0 a ako to súvisí
z lokalizovanými stavmi na takejto potenciálovej jame?
Dobrá rada: Opatí sa, po napísaní podmienok
diferencovateľnosti a spojitosti vlnovej funkcie v bodoch
nespojitosti potenciálu, pristupovať z nasledovnou
úvahou: (1) Ak častica dopadá s amplitúdou
E na miesto nespojitosti, s akou amlitúdou sa odráža?
t.j. vyjadriť F = f(E), paralelne s tým samozrejme
získame aj E = f(C) a F = f(C). (2) Ak častica
dopadá s amplitúdou A na miesto nespojitosti, s akou
amlitúdou sa odráža? Kompltné riešenie
je prístupné v PDF dokumente na www KF(
 ).
).
Figure:
Situácia pri rozptyle častice na
bariére (jame).
![\begin{figure}
\begin{center}
\includegraphics [angle=0,width=8cm]{Square-potential.eps}
\end{center} \end{figure}](Square-potential.jpg) |
- 20.
- Kvalitatívnou úvahou (pomocou princípu neurčitosti)
odhadnite pre akú bariéru (ako vysokú, ako širokú)
je pravdepodobnosť
tunelovania častice relatívne veľká, porovnajte
s presnými výsledkami predchádzaujúceho
príkladu. Ak vieme, že rozhranie kov-kov predstavuje
bariéru o veľkosti
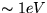 , odhadnite
šírku takéhoto rozhrania, ak vieme,
že elektróny bežne 'tunelujú'.
, odhadnite
šírku takéhoto rozhrania, ak vieme,
že elektróny bežne 'tunelujú'.
- 21.
- Cvičenie na H atóm. Nájdite 'prirodzené'
atómové jednotky pre problém elektrónu
v atóme vodíka (a teda pre akýkoľvek
Coulombický elektrónový problém).
Ako vyzerá elektrostatické pole generované
atómom vodíka ak ten sa nachádza v základnom
stave? (Vlnová funkcia
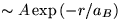 .)
.)
![]() ]
]
![]() ]
]
![]() ]
]![]() a riešte el.mag. pole v takomto prostredí.]
a riešte el.mag. pole v takomto prostredí.]
![]()
![]()
![[*]](/pics/cross_ref_motif.gif) )
vyčísliteľný. Pohyb častice zrejme zodpovedá
pohybu maxima tohto balíka.
)
vyčísliteľný. Pohyb častice zrejme zodpovedá
pohybu maxima tohto balíka.
![]() , čo má polohu maxima
danú
, čo má polohu maxima
danú ![]() .
.
![[*]](/pics/cross_ref_motif.gif) ) na koeficienty
aij?
) na koeficienty
aij?
![[*]](/pics/cross_ref_motif.gif) ) je špeciálna
Lorentzova transformácia. Inač povedané, vlnová
rovnica s fázovou rýchlosťou vf=c je relativisticky
invariantná.]
) je špeciálna
Lorentzova transformácia. Inač povedané, vlnová
rovnica s fázovou rýchlosťou vf=c je relativisticky
invariantná.]
![[*]](/pics/cross_ref_motif.gif) ) nájdite
relativistický vzťah pre Dopplerov effekt. Pomôcka:
Musí zrejme platiť
) nájdite
relativistický vzťah pre Dopplerov effekt. Pomôcka:
Musí zrejme platiť ![]() , kde
, kde ![]() je frekvencia v pohybujúcej sa sústave.]
je frekvencia v pohybujúcej sa sústave.]
![]() ,
, ![]() ,
, ![]() ,
kde
,
kde ![]() = eE/m0c,
= eE/m0c, ![]()
![]() , pričom pre základný stav
, pričom pre základný stav ![]() a
podobne
a
podobne ![]() . Uvážením
. Uvážením
![]() , má
, má ![]() minimum
pre
minimum
pre ![]() . To dáva 'prekvapivo' dobrý výsledok
. To dáva 'prekvapivo' dobrý výsledok
![]() .
.
![]() = E
= E ![]() ) = (zámena x -> -x) ( H(-x)
) = (zámena x -> -x) ( H(-x)
![]() = E
= E ![]() ) = (symetria H(x)) ( H(x)
) = (symetria H(x)) ( H(x) ![]() =
E
=
E ![]() ).
Posledná rovnosť znamená, že
).
Posledná rovnosť znamená, že ![]() a
a ![]() majú rovnakú vlastnú energiu, t.j.
majú rovnakú vlastnú energiu, t.j. ![]() .
Pretože
.
Pretože ![]() dostávame
c =
dostávame
c = ![]() 1. To znamená, že každá vlastná
funkcia H je buď párna alebo nepárna.
1. To znamená, že každá vlastná
funkcia H je buď párna alebo nepárna.
![[*]](/pics/cross_ref_motif.gif) )). Vlna s A
reprezentuje dopadajúcu časť vlnovej funkie, B
odrazenú a C prechádzajúcu. Pre aké energie
(vlnové
dĺžky) nedochádza ku odrazu? Pre aké energie
dochádza ku rezonancii, t.j. pre nekonečne malú
amplitúdu dopadajúcej vlny A je C aj B konečne
veľké? Ako je situácia závislá od rozdielu
energii voľnej častici E a potenciálom Vo?
Ako sa zmení situácia, pre Vo < 0 a ako to súvisí
z lokalizovanými stavmi na takejto potenciálovej jame?
)). Vlna s A
reprezentuje dopadajúcu časť vlnovej funkie, B
odrazenú a C prechádzajúcu. Pre aké energie
(vlnové
dĺžky) nedochádza ku odrazu? Pre aké energie
dochádza ku rezonancii, t.j. pre nekonečne malú
amplitúdu dopadajúcej vlny A je C aj B konečne
veľké? Ako je situácia závislá od rozdielu
energii voľnej častici E a potenciálom Vo?
Ako sa zmení situácia, pre Vo < 0 a ako to súvisí
z lokalizovanými stavmi na takejto potenciálovej jame?
 ).
).

![\begin{figure}
\begin{center}
\includegraphics [angle=0,width=8cm]{Square-potential.eps}
\end{center} \end{figure}](Square-potential.jpg)