|
Obr.
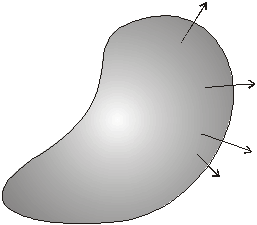
6.1.12.1 . Výtok vektora E z uzavretej plochy S
|
Pokúsime sa
teraz zistiť, či tento výsledok platí celkom všeobecne. Uvažujme nejaký objem V ohraničený uzavretou plochou S. V ňom sa nachádza elektrický náboj,
ktorý je spojito rozložený s objemovou hustotou r. Situáciu znázorňuje obr. 6.1.12.1.
Podľa
Gaussovej vety platí
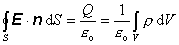 (6.1.104)
(6.1.104)
V prvej
kapitole vo vektorovom počte sme sa dozvedeli, že za istých podmienok (diferencovateľnosť
funkcií, hladká plocha atd.) je možné plošný integrál previesť na objemový.
Platí
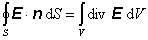 (6.1.105)
(6.1.105)
kde V je objem uzavretý plochou
S. Tento matematický vzťah sa v literatúre nazýva Gauss-Ostragradského
veta, alebo Gaussova veta vektorového počtu. Ak aplikujeme túto matematickú
transformáciu na ľavú stranu rovnice (6.1.104), tak dostaneme
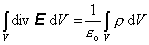 (6.1.106)
(6.1.106)
Rovnicu
môžem prepísať nasledovne
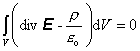 (6.1.107)
(6.1.107)
Pritom
plochu S, resp. objem V, ktorý je ňou ohraničený možno voliť celkom
ľubovoľne. To ale znamená, že integrand v rovnici (6.1.107) musí byť
identický rovný nule. Nie je totiž možné, aby integrand bol v jednej časti
priestoru kladný a inde záporný a tým by sa príspevky k integrálu kompenzovali,
lebo už pri malej zmene objemu V by
rovnica potom prestala platiť. Tým dostávame elegantný výsledok
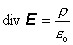 (16.1.08)
(16.1.08)
Toto je prvá
Maxwellova rovnica pre elektrostatické pole vo vákuu. Rovnica hovorí, že divergencia
intenzity elektrického poľa sa rovná podielu hustoty náboja a permitivity vákua.
Pre
elektrostatické pôsobenie nábojov je typický centrálny charakter elektrických
síl. V dôsledku toho má vektor poľa radiálny smer a vďaka tomu sme mohli
zaviesť elektrický potenciál. Skúsme teraz vytvoriť dve rôzne integračné cesty
medzi bodmi A, B.
|
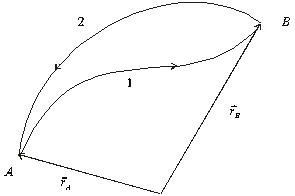
Obr. 6.1.12.2 Dve
integračné cesty medzi bodmi A, B
|
V
elektrostatickom poli platí
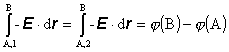 (6.1.109)
(6.1.109)
Vytvorme
teraz uzavretú integračnú cestu C = A
® 1 ® B ® 2 ® A. Zrejme platí
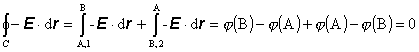 (6.1.110)
(6.1.110)
Keby rovnica
(6.1.110) neplatila, vedeli by sme nájsť takú cestu v elektrickom poli, že po
každom obehu by sme získali určitú energiu, čo by bolo v rozpore so zákonom zachovania
energie. Na druhej strane integrál z vektorovej funkcie po uzavretej krivke
možno podľa Stokesovej vety transformovať na plošný integrál, takže
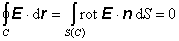 (6.1.111)
(6.1.111)
Ak uvážime,
že krivka C je celkom ľubovoľná, tak
rovnica (6.1.113) bude splnená iba tak, že jej integrand sa identický rovná
nule, čiže
rot E = 0 (6.1.112)
Rovnica
(6.1.112) predstavuje špeciálny prípad 4. Maxwellovej rovnice pre statické pole
E. Rovnica ukazuje, že elektrostatické pole nemá vírový charakter. Rovnice (6.1.108) a (6.1.112) úplne popisujú
všetky elektrostatické javy vo vákuu. Na týchto rovniciach sa najlepšie
odzrkadľuje nová kvalita popisu elektromagnetických javov prostredníctvom
veličín poľa. Zmeny elektrického poľa v okolí nejakého bodu závisia iba od lokálnej
hustoty elektrického náboja.