Vráťme sa teraz k príkladu s rovnomerne nabitou guľou o polomere R. Vo vnútri gule má elektrické pole E radiálny smer a jeho veľkosť lineárne vzrastá s polomerom r, teda
 (6.1.98)
(6.1.98)
V úvodnej kapitole vektorového počtu bola popri gradiente skalárnej
funkcie zavedená operácia divergencie vektorovej funkcie. Skúsme teraz vypočítať
divergenciu z poľa E vo
vnútri gule
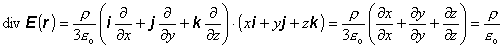 (6.1.99)
(6.1.99)
Mimo nabitej oblasti gule r >
R má pole E
tvar
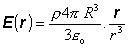 (6.1.100)
(6.1.100)
Vypočítajme divergenciu z tohoto výrazu:
 (6.1.101)
(6.1.101)
Dospeli sme k
celkom zaujímavému výsledku:
- V miestach, kde je náboj rozložený spojito s konštantnou hustotou r je
 (6.1.102)
(6.1.102)
- V miestach, kde nie je náboj
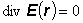 (6.1.103)
(6.1.103)
Vzťah (6.1.102) súvisí s našou konvenciou definície siločiar
elektrického poľa. Povedali sme, že siločiary vychádzajú z miesta kladného
náboja a vstupujú do miesta, kde je záporný náboj. To znamená, že všade tam,
kde sa nachádzajú nové náboje vznikajú nové siločiary. Týchto siločiar je tým
viac čím viac nábojov sa v danom mieste nachádza, t.j. čím je väčšia hustota náboja
v danom bode. Presne toto vyjadruje aj rovnica (6.1.102). Vo voľnom priestore,
kde nie sú žiadne náboje je div E = 0.
Vidíme, že veličina div E nám
znázorňuje vytekanie vektora elektrického poľa všade z tých miest, kde sa
nachádzajú náboje.