Postup
uvedený v predchádzajúcom odseku môžeme zovšeobecniť na ľubovoľnú sústavu
nábojov, ktorá je obmedzená na malú oblasť priestoru a potenciál budeme počítať
mimo tejto oblasti. Počiatok súradnicovej sústavy umiestnime do tejto
oblasti. V bodoch určených polohovými
vektormi a1, a2,… an sa nachádzajú náboje q1, q2,
..., qn. Pozri obr.
6.1.11.3.
|
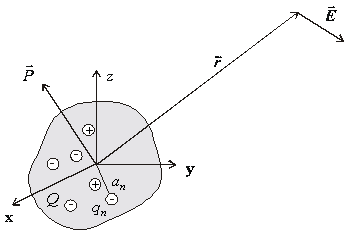
Obr. 6.1.11.3 Sústava bodových nábojov
|
Potenciál sústavy
v bode r je
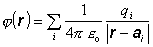 (6.1.88)
(6.1.88)
Vo väčších
vzdialenostiach od tejto sústavy je 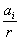 << 1. Potom
platí
<< 1. Potom
platí
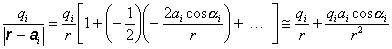 (6.1.89)
(6.1.89)
Výraz aicosai môžeme vyjadriť cez skalárny súčin vektora ai a polohového vektora r
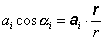 (6.1.90)
(6.1.90)
Potom pre
celkový potenciál dostaneme
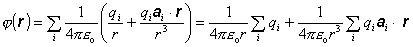 (6.1.91)
(6.1.91)
Vidíme, že
potenciál j sa skladá z dvoch členov. Prvý obsahuje súčet všetkých nábojov sústavy
Q = 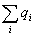 a klesá s 1. mocninou
vzdialenosti r. Druhý člen obsahuje
vektorový súčet výrazov qi ai, ktorý budeme označovať ako celkový “dipólový
moment” sústavy nábojov
a klesá s 1. mocninou
vzdialenosti r. Druhý člen obsahuje
vektorový súčet výrazov qi ai, ktorý budeme označovať ako celkový “dipólový
moment” sústavy nábojov
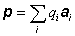 (6.1.92)
(6.1.92)
Výsledný potenciál sústavy je
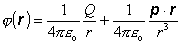 (6.1.93)
(6.1.93)
Keby sme v našom priblížení
akceptovali aj vyššie mocniny 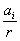 dostali by sme ďalšie
členy, ktoré odpovedajú vyšším momentom charakterizujúcim rozloženie náboja
(kvadrupól, oktupól atd.). Derivovaním výrazu (6.1.93) dostaneme ihneď vyjadrenie
pre elektrické pole sústavy
dostali by sme ďalšie
členy, ktoré odpovedajú vyšším momentom charakterizujúcim rozloženie náboja
(kvadrupól, oktupól atd.). Derivovaním výrazu (6.1.93) dostaneme ihneď vyjadrenie
pre elektrické pole sústavy
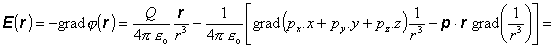
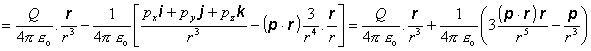 (6.1.94)
(6.1.94)
Často sa
stáva, že výsledný elektrický náboj sústavy Q
je rovný nule - sústava (teleso) je elektricky neutrálna, avšak vo výraze pre
pole zostáva príspevok od dipólového momentu p
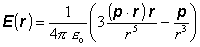 (6.1.95)
(6.1.95)
Ak zvolíme
osi súradnicovej sústavy tak, aby os z bola
rovnobežná so smerom dipólo-vého momentu p,
potom p = pk a
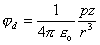 (6.1.96)
(6.1.96)
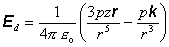 (6.1.97)
(6.1.97)
|
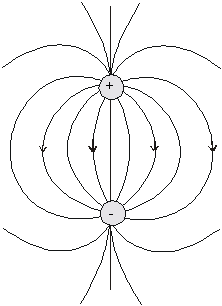
Obr.
6.1.11.4 Siločiary elektrostatického poľa dipólu.
|
Siločiary
elektrostatického poľa dipólu sú znázornené na obr. 6.1.11.4.