




1. Základné informácie o vektoroch
1.1 Úvodné pojmy
Vo fyzike a technických disciplínach sa stretávame s veličinami, na úplné určenie ktorých postačuje zadať jedinú číselnú hodnotu. Pre takéto veličiny, medzi ktoré patria napr. teplota, hmotnosť, alebo objem, používame názov skalárne veličiny (stručne skaláry). Často sa však stretávame s veličinami, ktoré charakterizujeme nie iba ich veľkosťou, ale aj smerom v priestore. Nazývame ich vektorové veličiny (stručne vektory). Navyše je pre ne typický spôsob sčitovania, ktorý geometricky znázorňujeme pomocou skladania úsečiek. Medzi vektorové veličiny patrí napríklad rýchlosť, sila, alebo intenzita elektrického poľa. Na úplné určenie vektorovej veličiny v trojrozmernom
priestore, vzhľadom na potrebu vyjadriť nie iba jej veľkosť, ale aj smer, treba zadať tri číselné hodnoty, ktorým hovoríme súradnice vektora (vektorové súradnice).
Vektory sa zapisujú tučnými písmenami, napr. a, E, r
, alebo označujú šipkou nad písmenom : 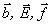 . Značky všetkých veličín, teda aj vektorových, sa podľa
normy STN ISO 31-0 majú písať ležatým písmom - kurzívou. . Značky všetkých veličín, teda aj vektorových, sa podľa
normy STN ISO 31-0 majú písať ležatým písmom - kurzívou.
Veľkosť vektorových veličín sa zapisuje jednoduchým písmom (nie tučným, resp. bez šipky nad písmenom) : b, E, f , alebo sa vektor vloží mezi značky vyjadrujúce absolútnu hodnotu : |
a|
, |
E|
, resp. 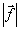 . Veľkosť vektora sa nazýva aj absolútna hodnota, je vždy nezáporná. . Veľkosť vektora sa nazýva aj absolútna hodnota, je vždy nezáporná.
Graficky sa vektorové veličiny znázorňujú úsečkou, so šipkou na jednom konci úsečky.
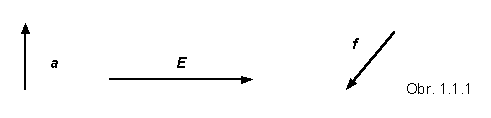
Miesto na úsečke opatrené šipkou sa považuje za "koniec vektora", na opačnej strane úsečky je "začiatok vektora".
Vektory rovnobežné s jednou priamkou nazývame kolineárne, vektory rovnobežné s jednou rovinou komplanárne. Kolineárne vektory môžu mať
rovnaký, alebo navzájom opačný smer.
Dva vektory považujeme za rovnaké , ak
majú rovnaký smer a rovnakú veľkosť (sú teda kolineárne) .
Súčet dvoch vektorov a + b = c je operácia, ktorej výsledkom je opäť vektor. Graficky sa znázorňuje pomocou úsečiek zobrazujúcich vektory : ku koncu prvého vektora pripojíme druhý vektor, pričom výsledkom ich sčítania je tretí vektor, ktorého začiatok je zhodný so začiatkom prvého vektora a koniec s koncom druhého
vektora . V grafickom znázornení :
Analogicky sa pokračuje pri sčítaní viacerých vektorov.
Súčet vektorov je komutatívna operácia, čiže výsledok súčtu nezáleží na poradí skladania vektorov :
a + b = b + a . (1.1.1)
Pri sčítaní viacerých vektorov sa uplatňuje asociatívnosť, ktorú v prípade troch vektorov možno vyjadriť vzťahom
a + b + c = (a + b) + c = a + (b + c) (1.1.2)
Ak pred vektor napíšeme znamienko "mínus", napríklad -a , podľa pravidiel vektorovej algebry to predstavuje vektor, ktorý má rovnakú veľkosť ako vektor a , ale má opačný smer. Nový vektor možno označiť ako vektor b, a zapísať rovnosť b = -a . Vektory a , b sú teda kolineárne. Takéto označenie umožňuje zaviesť odčítanie (rozdiel) vektorov. Rozdiel vektorov c - d = f chápeme ako súčet vektorov c a (-d), t.j. f = c + (-d) .
Rovnicu c - d = f možno upraviť rovnako, ako rovnicu s obyčajnými číslami, napríklad vektor d previesť na pravú stranu rovnice : c = d + f . Takto upravená rovnica môže poslúžiť na overenie správnosti vykonanej operácie.
Príklad 1.1.1
Dva nekolineárne vektory, napr. a, b , môžeme chápať ako strany rovnobežníka. Graficky ukážte, že ich súčet a rozdiel predstavujú uhlopriečky tohto rovnobežníka. Riešenie :
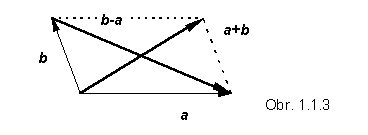
Súčet vektorov má časté uplatnenie v praxi. Napríklad sčítaním rýchlosti lode vzhľadom na vodu s rýchlosťou vody v rieke, dostaneme rýchlosť lode vzhľadom na breh rieky.
Násobenie vektora číslom je operácia, ktorá poskytne nový vektor so zmenenou
veľkosťou, ale kolineárny s pôvodným vektorom. Napríklad vynásobením vektora
a číslom 3 získame vektor b s trojnásobnou veľkosťou a nezmeneným smerom. Ak však vektor a budeme násobiť číslom - 0,5 , dostaneme vektor c s polovičnou veľkosťou, navyše s
opačným smerom. Je to ďalšie pravidlo vektorovej algebry. Všeobecne tento vzťah
zapisujeme v tvare
b = sa , (1.1.3)
kde s môže predstavovať nie iba bezrozmerné číslo, ale aj skalárnu veličinu. Napríklad v kinematike sa stretneme s výrazom vt , teda súčinom vektora rýchlosti a času. Tak dostaneme novú fyzikálnu veličinu, ktorej veľkosť a fyzikálny rozmer sú súčinom veľkostí, resp. rozmerov vektorovej a skalárnej veličiny. V literatúre o vektorovom počte sa táto operácia nazýva skalárny násobok vektora.
Jednotkový vektor má veľkosť rovnajúcu sa číslu 1, je bezrozmerný. S výhodou ho možno použiť na vyjadrenie viacerých vektorov, ktoré sú s ním rovnobežné. Nech j je jednotkový vektor, a nech vektory a, b, c sú s ním súhlasne rovnobežné. Preto ich možno vyjadriť ako skalárne násobky jednotkového vektora, pričom skalármi, ktorými jednotkový vektor násobíme, sú veľkosti týchto vektorov : a = a j , b = b j , c = c j . Situácia sa môže skomplikovať, ak niektorý z vektorov má opačný smer ako jednotkový vektor. Vtedy pred skalárny násobok vektora j treba pripísať znamienko "mínus".
(Pozri ďalej - rozklad vektora, súradnice vektora).
Príklad 1.1.2
Nakreslite štvoruholník, ktorého strany nie sú rovnako dlhé. Dokážte, že ak by sa uhlopriečky štvoruholníka pretínali vo svojich stredoch, musel by to byť rovnobežník. (Obr. 1.1.4) 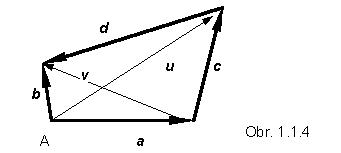
Riešenie : Najprv treba označiť všetky štyri strany štvoruholníka ako vektory. Podľa obrázku dokážeme určiť vektory smerujúce z vrcholu A do stredov uhlopriečok. Do stredu uhlopriečky u smeruje vektor p = (1/2) u = (1/2)(a + + c) a do stredu uhlopriečky v vektor
q = a + (1/2)(b - a) = (1/2)(a + b) .
Ak majú byť stredy uhlopriečok totožné, musia byť vektory p a q rovnaké :
(1/2)(a + c) = (1/2)(a + b) ,
z čoho bezprostredne vyplýva rovnosť vektorov b a c . Majú teda rovnakú veľkosť aj smer, preto sú rovnobežné, tvoria dve strany rovnobežníka. Výsledok pre ďalšie dve strany získame úvahou o vektore u. Platí u = c + a a súčasne u + d = b, čiže u = b - d a s využitím rovnosti b = c aj u = c - d . Porovnaním dvoch vyjadrení vektora u dospejeme k výsledku a =
- d . Teda aj tieto vektory sú
rovnobežné, majú rovnakú veľkosť, ale opačný smer.
Rozklad vektora na zložky je opačná operácia ako súčet vektorov. V rovine možno
vektor rozložiť na dve zložky, t.j. na dva vektory do vopred určených smerov.
Sčítaním zložiek vznikne pôvodný vektor. Na obr. 1.1.5 je znázornený rozklad vektora a do smerov naznačených dvomi priamkami. Uskutočňuje sa tak, že priamky, do smerov ktorých treba vektor rozložiť, vedieme koncovým aj začiatočným bodom vektora. Tak vznikne rovnobežník, na ktorom už jednoducho vyznačíme zložky p a q .
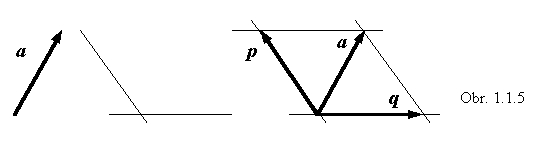
V priamkach, do ktorých rozkladáme vektor a , môžeme zvoliť jednotkové vektory, ktoré označíme e1 a e2 . Jednotkovými vektormi sú potom určené príslušné smery. Zložky p a q vyjadríme ako skalárne násobky vektorov e1 a e2 : p = ape1 , q = aqe2 . Vektor e1 však môže mať opačný smer ako zložka p , a vtedy skalár ap pred vektorom e1 musí byť záporný. Preto skalár ap nepredstavuje veľkosť vektora p, ale je jednou zo súradníc rozloženého vektora a vo vzťažnej sústave určenej vektormi e1 a e2 . Vektor a možno po takomto rozklade na zložky vyjadriť v tvare a = p + q = ape1 + aqe2 . (1.1.4)
O takomto vyjadrení hovoríme, že vektor a je lineárnou kombináciou vektorov e1 a e2 .
V trojrozmernom priestore musí byť vzťažná sústava určená tromi vektormi e1 , e2 a e3 , o ktorých hovoríme, že tvoria jej bázu . Vo všeobecnosti to ani nemusia byť jednotkové vektory. Najčastejšie sa však používa rozklad do troch navzájom kolmých smerov, určených jednotkovými vektormi so zaužívaným označením i, j, k . Stotožňujú sa so smermi súradnicových osí x, y, z karteziánskej súradnicovej sústavy. Ľubovoľný vektor f možno pomocou takejto trojice jednotkových vektorov vyjadriť ako ich lineárnu kombináciu
f = fx i + fy j + fz k . (1.1.5)
V tomto vyjadrení vektora f sú fx , fy a fz jeho súradnice, ktoré môžu byť kladné, i záporné podľa toho, aký je jeho smer vzhľadom na jednotkové vektory. Na obr. 1.1.6 je znázornený dvojrozmerný prípad, pričom vektor g má zápornú súradnicu gx , ostatné súradnice vektorov f a g sú kladné.
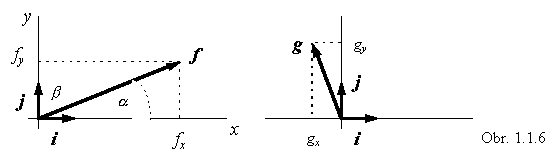
Veľkosť vektora f
možno v karteziánskej súradnicovej sústave vyjadriť pomocou jeho súradníc,
použitím Pythagorovej vety
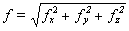 . (1.1.6) . (1.1.6)
Vektor f zviera s vektormi i, j, k smerové uhly a
, b
, g
, pre ktoré platia vzťahy 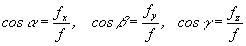 , (1.1.7) ktoré si možno overiť na dvojrozmernom obrázku 1.1.6 . , (1.1.7) ktoré si možno overiť na dvojrozmernom obrázku 1.1.6 .
Zo vzťahov (1.1.7) pre kosínusy smerových uhlov ( smerové kosínusy) bezprostredne vyplýva rovnosť
cos2a
+ cos2b
+ cos2g
= 1 (1.1.8)
Súčet vektorov vyjadrených v zložkách
Keď vyjadríme dva vektory pomocou ich
súradníc : a = ax i + ay j + az k , b = bx i + by j + bz k môžeme ich súčet uskutočniť po zložkách, na základe platnosti komutatívnosti a asociatívnosti súčtu vektorov : a + b = ( ax+ bx) i + (ay + by) j + (az + bz ) k , (1.1.9)
takže pre súradnice výsledného vektora c platí
cx = ( ax+ bx) , cy = (ay + by) , cz = (az + bz ) . (1.1.10)
Pre skalárny násobok vektora vyjadreného v zložkách platí :
sa = s ( ax i + ay j + az k ) = sax i + say j + saz k (1.1.11)
Príklad 1.1.3 Vypočítajte súčet vektorov a = 3 i + 2 j - k a b =
-i + 2 j - 2 k .
Riešenie : c = a + b = (3 - 1)i + (2 + 2)j + (-1 -3)k = 2 i + 4j - 3k , takže súradnice vektora c sú : cx = 2 , cy = 4 , cz = -3 .
Príklad 1.1.4 Vyjadrite vektor d, ktorý má trojnásobnú veľkosť a opačný smer ako vektor a = 3 i + 2 j - k .
Riešenie : d = (-3)a = (-3)(3 i + 2 j - k ) = -9 i - 6 j + 3k . Presvedčte sa , že veľkosť vektora d je naozaj trojnásobná v porovnaní s veľkosťou vektora a .
Kontrolné otázky k časti 1.1
- Dva vektory, ktoré majú rovnakú veľkosť a rovnaký
smer, nemajú spoločný začiatočný bod. Sú takéto vektory rovnaké ?
- Dva rovnobežné vektory majú vzájomne opačný
smer. Sú kolineárne
?
Kedy sú vektory komplanárne ?
Závisí výsledok súčtu dvoch, prípadne
viacerých vektorov od poradia v ktorom ich sčitujeme ?
Možno rozdiel dvoch vektorov vyjadriť pomocou
vektorového súčtu ?
Ako možno z daného vektora vytvoriť vektor
opačného smeru, navyše s päťnásobnou veľkosťou ? Ako sa príslušná operácia
nazýva ?
Aké vlastnosti má jednotkový vektor ?
Získame súčtom dvoch vzájomne kolmých
jednotkových vektorov opäť jednotkový vektor ?
Ako rozkladáme vektor (v rovine) do dvoch
vopred zadaných smerov ?
Možno vektor rozložiť do dvoch smerov, ktoré zvierajú uhol väčší než 90 o ?
Uveďte čo rozumieme pod lineárnou
kombináciou vektorov !
Možno vektor vyjadriť ako lineárnu
kombináciu vektorov, ktoré nie sú jednotkové ?
Čo je to báza vo vzťažnej sústave ?
Aký je rozdiel medzi zložkami a súradnicami
vektora ?
Čo sú smerové uhly a smerové kosínusy
vektora ?
Ako vypočítame veľkosť vektora, keď poznáme
jeho súradnice v karteziánskej súradnicovej sústave ?
Ak poznáme súradnice dvoch vektorov, ako vypočítame súradnice vektora, ktorý vznikne ich súčtom ?
|