Budeme sa venovať rozdeleniu častíc plynu vo vertikálnom stĺpci s prierezom S. Zvolíme si os y smerujúcu nahor. Ďalej budeme predpokladať, že teplota plynu je všade tá istá. V stĺpci si predstavíme vrstvu, ktorá je vo výške y a má hrúbku dy. Táto vrstva je v rovnováhe, čo znamená že sily, ktoré na ňu pôsobia vo zvislom smere sa navzájom kompenzujú. Pôsobia tu sily: tiaž vrstvy dm.g, smerujúca nadol, tlaková sila pôsobiaca na spodnú základňu pS smerujúca nahor a tlaková sila pôsobiaca na hornú základňu (p+dp).S smerujúca nadol. Tlakové sily sú spôsobené nárazmi častíc plynu na myslené základne, t.j. sú dôsledkom tepelného pohybu častíc. Súčet síl pôsobiacich na vrstvu plynu je

,

odkiaľ

(a).

Zo stavovej rovnice ideálneho plynu máme pV = N kT , kde N je počet častíc v objeme V (pozri § 4.1.4). Odtiaľto vyplýva

, (b)

kde n je koncentrácia častíc. V našom prípade je dp = kTdn, lebo T = const. Hmotnosť vrstvy je dm = nm₀ dV =nm₀Sdy, kde m₀ je hmotnosť jednej častice.

Po dosadení do (a) kTdnS = - nm₀ gSdy ,

odkiaľ

.

Po integrovaní

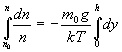
dostaneme

. (4.1.18)