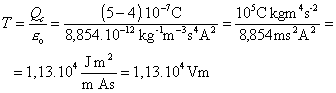6.1.9.1 Tok elektrického poľa bodového náboja pri všeobecnom tvare plochy S

Uvažujme celkom všeobecnú plochu S, ktorá obklopuje náboj q_i. Plochu rozdelíme na malé plôšky dS, v rozsahu ktorých je vektor poľa E konštantný. Ak každým okrajovým bodom plôšky dS vedieme priamku, ktorá prechádza bodovým nábojom q_i, tak dostaneme kužeľovú plochu, ktorá pri svojom vrchole definuje priestorový uhol dw.

Priestorový uhol w definujeme podľa analógie uhla v rovine ako podiel veľkosti plochy S na povrchu gule o polomere r, ktorú kužeľová plocha obopínajúca priestorový uhol w vytína,  ku kvadrátu polomeru r. Plný priestorový uhol W  vypočítame ako veľkosť povrchu gule s jednotkový polomerom, čiže W = 4p 1² = 4p. Príspevok od plôšky dS k toku elektrického poľa je

dY_i = E . n dS = E dS . cos a = dS´                                                                      (6.1.36)

súčin dS . cos a však môžeme interpretovať ako veľkosť priemetu plôšky dS do roviny, ktorá je kolmá na vektor r = r - r_i. Tento priemet sme označili ako dS´. Na základe definície priestorového uhla zrejme platí

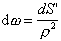                                                                                                                         (6.1.37)

alebo obrátene

                    dS´ = r²dw                                                                                                   (6.1.38)

Pokiaľ má plocha S taký tvar, že každá polpriamka vychádzajúca z bodového náboja q_i ju pretína iba raz (v jedinom bode), tak normála n je orientovaná od náboja q_i a cosa je kladný. Potom sčítanie príspevkov od všetkých elementov dS je jednoduché

                     (6.1.39)

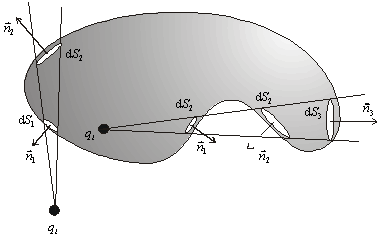
Vo všeobecnosti však musíme predpokladať zložitejší tvar plochy S a pri záhyboch tejto plochy sa budú vyskytovať príspevky, kde cosa  bude mať ako kladné tak aj záporné hodnoty. Pozri obr. 6.1.8.2

 

 

Pre jeden kužeľ obopínajúci uhol dw sú všetky príspevky E .dS´, E . dS´´, ...., čo do absolútnej hodnoty rovnaké, lebo r² v menovateli pre E sa vyruší s členom r² vo výraze dS´= r² dw. Znamienko takéhoto príspevku závisí od lokálnej orientácie normály n. Môžu nastať dva prípady:

 

1.  Náboj q_i sa nachádza vo vnútri plochy S.

V mieste prvého príspevku k dY vektor r vychádza zvnútra plochy S von, normála n je orientovaná od náboja q_i a teda cosa > 0. V mieste ďalšieho príspevku E.n dS´´  už vektor r prechádza z vonkajšej strany plochy S dovnútra, normála n smeruje k náboju q_i a znamienko príspevku je záporné. Vektor r takto pretína plochu S v nepárnom počte bodov, a preto párny počet rovnakých príspevkov s opačnými znamienkami sa vyruší a do výsledku zostáva iba prvý z nich. Teda

                                                                                                                        (6.1.40)

 

2.      Náboj q_i sa nachádza mimo plochy S

Zopakujeme tú istú úvahu ako v predchádzajúcom prípade. Rozdiel je len v tom, že vektor r pretína plochu S v párnom počte bodov, takže všetky príspevky k dY  sa v konečnom dôsledku vyrušia a výsledok je rovný nule. Teda

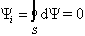
                                                                                                                 (6.1.41)

_________________________________________________________________________________

Príklad 6.1.8.1

Dva náboje –4.10^-7 C a 5.10^-7 C sú vo vzdialenosti 10 cm. Náboje sa nachádzajú vo vákuu.

a)       Akou silou na seba pôsobia ?

b)       Aký je tok vektora intenzity elektrostatického poľa cez plochu, ktorá obklopuje obidva tieto náboje?

Riešenie:

a)          =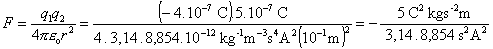

 

= 1, 8. 10^-1 N

 

b)