Doplnok úloh z kinematiky a dynamiky hmotného bodu a z elektrostatiky


Úlohy sú vybraté z nasledujúcich učebníc :


FEYNMAN, R. P., LEIGHTON, R. B., SANDS, M. Fejmanovskie lekcii po fizike.

Zadači i upražnenia s otvetami i rešeniami (pod obščej redakciej A. P. Levanjuka).

Moskva: Mir, 1969

HALLIDAY, D., RESNICK, R., Walker, J. Fundamentals of Physics. 5nd ed. New York: John Wiley Sons, Inc., 1997

   IRODOV, I. E. Osnovnyje zakony elektromagnetizma. Moskva. Vysšaja škola, 1983

   IRODOV, I. E. Zadači po obščej fizike. Moskva. Nauka, 1988

SIVUCHIN, D. V. Obščij kurs fiziki, TomIII, Električestvo. 2. vyd. Moskva: Nauka, 1983

Mechanika hmotného bodu


Kinematika


K1. Dve častice 1 a 2 sa pohybujú konštantnými rýchlosťami po dvoch na seba kolmých priamkach k bodu ich pretnutia O . V čase boli od bodu O vzdialené o . V akom čase bude vzdialenosť oboch častíc najmenšia ? Túto vzdialenosť aj vypočítajte !

Odpoveď: .


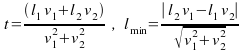K2. Z bodu A na asfaltovej ceste sa treba čo najrýchlejšie prepraviť na aute do bodu B v poli, ktorý je od cesty vzdialený l . Je známe, že rýchlosť auta po poli je násobkom rýchlosti na ceste ( 1). V akej vzdialenosti b od bodu D máme odbočiť do poľa ?

(Odpoveď: )


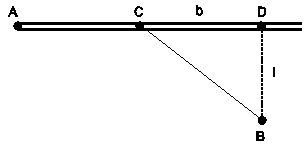
K3. Dve častice sa pohybujú so zrýchlením g v homogénnom gravitačnom poli Zeme. V počiatočnom momente sa častice nachádzali v tom istom bode, keď sme im udelili počiatočnú rýchlosť v horizontálnom smere na opačné strany. Vypočítajte vzdialenosť častíc v okamžiku, keď sú vektory ich rýchlostí na seba kolmé !

Odpoveď: .


K4. Polohový vektor častice sa mení s časom podľa vzťahu , kde - konštantný vektor, - konštanta. Najdite:

a) rýchlosť a zrýchlenie ako funkcie času,

b) časový interval , po ktorom sa častica vráti do východzej polohy a

c) dráhu s , ktorú pritom prejde.

Odpoveď: a) zrejmé, b) .


K5. Častica sa pohybuje po priamke spomalene so zrýchlením, ktoré závisí od rýchlosti ako funkcia , kde k je kladná konštanta. Na začiatku pohybu mala častica rýchlosť . Aký kus dráhy prejde častica do zastavenia ? Za aký čas prejde túto dráhu ?

Odpoveď: .


K6. Polohový vektor bodu A sa vzhľadom na začiatok vzťažnej sústavy mení s časom podľa vzťahu , kde sú konštanty, sú jednotkové vektory v smere osí X a Y. Najdite:

a) rovnicu trajektórie

b) časové závislosti rýchlosti a veľkosti týchto veličín

c) časovú závislosť uhla medzi vektormi.

Odpoveď: a) , b) zrejmé, c) .


K7. Bod sa pohybuje v rovine XY podľa vzťahov kde A a sú kladné konštanty. Nájsť:

a) dráhu s , ktorú bod prejde za čas ,

b) uhol medzi rýchlosťou a zrýchlením.

Odpoveď: a) .


K8. Pod akým uhlom k horizontu treba hodiť guľu, aby :

a) polomer krivosti jej trajektórie na začiatku bol krát väčší ako v maximálnej výške na trajektórii,

b) stred krivosti trajektórie v maximálnej výške dráhy sa nachádzal na povrchu Zeme ?

Odpoveď: a).


K9. Guľôčka padá s nulovou počiatočnou rýchlosťou na hladkú naklonenú rovinu odklonenú od horizontálnej roviny o uhol a pružne sa od nej odrazí po prelete výšky h.V akej vzdialenosti od miesta dopadu sa na naklonenej rovine odrazí od nej druhýkrát ?

Odpoveď: .


K10. Delo a cieľ sa nachádzajú na jednej výškovej úrovni vo vzdialenosti 5,1 km. Za aký čas náboj trafí cieľ, ak má počiatočnú rýchlosť ?

Odpoveď: existujú dve riešenia: .


K11. Vzdušný balón sa začne dvíhať zo zemského povrchu, pričom rýchlosť vzostupu (nahor) je konštantná a rovná . Vplyvom vetra balón nadobúda horizontálnu zložku rýchlosti kde je kladná konštanta a y – výška nad zemou. Najdite:

a) veľkosť horizontálneho unesenia balóna

b) veľkosť celkového, tangenciálneho a normálového zrýchlenia .

Odpoveď: a), b) .


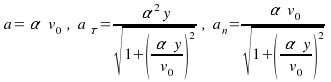K12. Častica sa pohybuje v rovine XY rýchlosťou , kde x , y sú súradnice častice, - konštanty. V čase sa častica nachádzala v začiatku vzťažnej sústavy. Najdite :

a) rovnicu trajektórie

b) polomer krivosti trajektórie v závislosti od x , t.j. .

Odpoveď: a) b) .


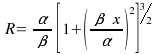K13. Častica A sa pohybuje na jednu stranu od začiatku O (obrázok) s tangenciálnym zrýchlením k . , kde je konštantný vektor paralelný X – ovej osi a je jednotkový dotykový vektor k trajektórii častice v smere narastania dĺžky dráhy. Najdite veľkosť rýchlosti častice v závislosti od x , ak v bode bola jej rýchlosť nulová .

Odpoveď: .


K14. Bod sa pohybuje spomalene po kružnici s polomerom R tak, že v každom časovom momente sú si rovné veľkosti tangenciálneho a normálového zrýchlenia. V čase bola rýchlosť bodu . Najdite závislosti :

a) rýchlosť bodu od času a od prejdenej dráhy s ,

b) celkové zrýchlenie bodu od rýchlosti a prejdenej dráhy !

Odpoveď: a) .


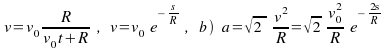K15. Častica sa pohybuje po kružnici s polomerom R tak, že jej rýchlosť závisí od prejdenej dráhy s podľa vzťahu , kde k 0 je konštanta. Najdite uhol medzi vektorom rýchlosti a (celkového) zrýchlenia v závislosti od s !

Odpoveď: .


K16. Častica A sa pohybuje po kružnici s polomerom R tak, že jej polohový vektor vzhľadom na bod O (obrázok) sa stáča uhlovou rýchlosťou . Najdite veľkosť rýchlosti častice a tiež veľkosť zrýchlenia a aj jeho smer !

Odpoveď: .


K17. Tuhé teleso spomalene rotuje okolo pevnej osi s uhlovým zrýchlením , úmerným (čo do veľkosti) , kde je uhlová rýchlosť otáčania telesa. Najdite strednú uhlovú rýchlosť za dobu otáčania telesa (t.j. po hodnotu ), keď počiatočná uhlová rýchlosť bola.

Odpoveď: .


K18. Loď sa pohybuje po rovníku na východ rýchlosťou . Z juhovýchodu pod uhlom k rovníku fúka vietor rýchlosťou . Najdite rýchlosť vetra vzhľadom na loď a uhol medzi rovníkom a smerom vetra v referenčnej sústave viazanej na loď.

Odpoveď: .


K19. Guľa s polomerom sa valí bez šmýkania po horizontálnej rovine tak, že jej stred sa pohybuje s konštantným zrýchlením . Po čase od začiatku pohybu (z pokoja) jej polohu ukazuje obrázok. Vypočítajte :

a) rýchlosť bodov A a B (veľkosti),

b) veľkosť zrýchlení bodov A a O (sú to body gule) .

Odpoveď: .


K20. Tuhé teleso rotuje okolo horizontálnej osi s konštantnou uhlovou rýchlosťou . V čase sa táto os začne otáčať okolo vertikálnej osi s konštantným uhlovým zrýchlením . Najdite veľkosti uhlovej rýchlosti a uhlového zrýchlenia telesa v čase . (Nakreslite si obrázok !)

Odpoveď: .


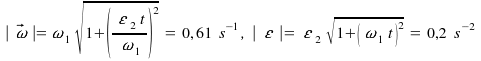K21*. Dve tuhé telesá rotujú okolo pevných, vzájomne kolmých pretínajúcich sa osí s konštantnými uhlovými rýchlosťami .Vypočítajte uhlovú rýchlosť a uhlové zrýchlenie druhého telesa vzhľadom na prvé teleso.

Odpoveď: = 2 - 1 , = 2 1 , .





Dynamika



D1. Častica sa pohybuje v smere osi X podľa vzťahu , kde >0 , >0 sú konštanty. V momente na časticu pôsobí sila . Najdite hodnoty sily v bode obratu a v momente, keď sa častica znovu ocitne v bode .

Odpoveď: .


D2. Najdite silu pôsobiacu na časticu o hmotnosti m pri jej pohybe v rovine XY podľa vzťahov , kde sú konštanty.

Odpoveď: , kde smeruje do začiatku vzťažnej sústavy.


D3. V zariadení podľa obrázka sú telesá troch hmotností, pričo hmotnosť lanka a kolieska možno zanedbať a trenie na osi kolieska tiež. Najdite zrýchlenie a , ktorým sa pohybuje teleso smerom nadol a silu napínania lanka T medzi telesami , ak koeficient trenia medzi telesami a podkladom je k .

Odpoveď: .


D4. Na naklonenú rovinu s uhlom odklonu od horizontálnej roviny položíme kváder a udelíme mu počiatočnú rýchlosť najstrmšie smerom nahor a paralelne s naklonenou rovinou. Zistite, pri akom uhle prejde kváder smerom nahor najmenšiu vzdialenosť a vypočítajte ju, keď koeficient trenia medzi kvádrom a rovinou je k ?

Odpoveď: .


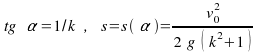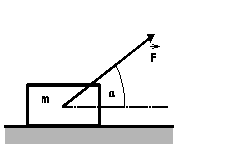
D5. Na teleso hmotnosti m , ležiace na hladkej horizontálnej rovine, začala v čase pôsobiť sila závisiaca od času podľa vzťahu , kde k > 0 je konštanta (obrázok). Najdite:

a) rýchlosť telesa v okamžiku odtrhu telesa od roviny,

b) dráhu, ktorú teleso prejde do tohoto momentu,

keď viete, že uhol sa s časom nemení !

Odpoveď: a) , b) .


D6. Ku kvádriku s hmotnosťou m , ležiacemu na hladkej horizontálnej rovine sme priložili silu so stálou veľkosťou . V procese jeho priamočiareho pohybu sa mení uhol medzi smerom tejto sily a horizontom podľa vzťahu , kde k > 0 je konštanta a s – dráha, ktorú kvádrik prešiel (od začiatku pohybu). Najdite rýchlosť kvádrika ako funkciu uhla .

Odpoveď: .


D7. Na stojacu časticu o hmotnosti m začala v čase pôsobiť sila závisiaca na čase podľa vzťahu , kde b je konštantný vektor a je doba, v priebehu ktorej sila pôsobí. Najdite:

a) hybnosť častice na konci pôsobenia sily,

b) dráhu, ktorú častica urazila za dobu pôsobenia sily.

Odpoveď: a) , b) .


D8. Guľôčka s hmotnosťou m je zavesená na niti a odchýlená do strany tak, aby napnutá niť vytvárala pravý uhol s vertikálou. Guľôčku potom voľne pustíme (t.j. bez udelenia počiatočnej rýchlosti). Treba nájsť:

a) veľkosť (celkového) zrýchlenia guľôčky a silu napínania nite T v závislosti od uhla medzi niťou a vertikálou,

b) silu napnutia nite v momente, keď je vertikálna zložka rýchlosti maximálna,

c) uhol v momente, keď je vektor zrýchlenia nasmerovaný horizontálne.

Odpoveď: a).


D9. Guľôčka, zavesená na niti, kmitá vo vertikálnej rovine tak, že sa jej zrýchlenia v krajnej (najvyššej) polohe a v najnižšej polohe čo do veľkosti rovnajú. Najdite uhol odklonenia nite v krajnej polohe od vertikály.

Odpoveď: , .


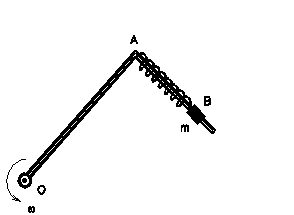
D10. Zariadenie na obrázku (pohľad zhora) je hladký drôt v tvare písmena , ktoré leží v horizontálnej rovine. Na ramene AB je nasunutá pružina s konštantou k . Pružina je pripevnená v mieste A a v mieste B je na ňu upevnené teleso v tvare valca o hmotnosti m nasunuté na drôt, po ktorom sa môže pohybovať bez trenia. Drôt roztočíme okolo vertikálnej osi idúcej cez bod O uhlovou rýchlosťou . Vypočítajte relatívne predĺženie pružiny ! Ako závisí výsledok od smeru rotácie ?

Odpoveď: .


D11. Cyklista jazdí po horizontálnej kruhovej plošine s polomerom R . Plošina je špeciálne upravená tak, že koeficient trenia závisí na nej iba od vzdialenosti r od stredu plošiny ako , kde je konštanta. Vypočítajte taký polomer r , po ktorej cyklista môže jazdiť najväčšou rýchlosťou. Aká je táto rýchlosť ?

Odpoveď: .


D12. Automobil sa pohybuje po horizontálnej kružnici s polomerom s konštantným tangenciálnym zrýchlením . Koeficient kinetického trenia medzi pneumatikami a podkladom je . Akú dráhu s prejde automobil do okamihu šmyku, keď počiatočnú rýchlosť mal nulovú ?

Odpoveď: .


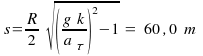D13. Cez kladku, upevnenú na strope miestnosti, je prevesené lanko, na koncoch ktorého sú zavesené závažia o hmotnostiach . Vypočítajte zrýchlenie hmotného stredu sústavy telies za predpokladu, že hmotnosti lanka a kladky sú zanedbateľné a tak isto aj trenie.

Odpoveď: .


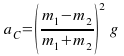D14. Cez kladku zavesenú na strope výťahovej kabíny je prevesené pevné lanko, na koncoch ktorého sú zavesené závažia o hmotnostiach a . Kabína výťahu sa začne pohybovať so zrýchlením . Pri zanedbaní hmotnosti lanka a kladky a tiež trenia, vypočítajte :

a) zrýchlenie závažia vzhľadom na kabínu,

b) silu , ktorou záves kladky ťahá na strop kabíny.

Odpoveď: a) , b) .


D15. Na rovníku z výšky padá na Zem teleso s nulovou počiatočnou rýchlosťou. Pri zanedbaní odporu vzduchu vypočítajte, o akú vzdialenosť s a na ktorú stranu dopadne teleso na Zem od vertikály ! Pri vyčíslení výsledku použite pre g hodnotu na rovníku .

Odpoveď: na východ, .


D16. Častica sa premiestnila po nejakej trajektórii v rovine XY z bodu 1 s polohovým vektorom do bodu 2 s polohovým vektorom . Pri pohybe na ňu pôsobili isté sily, z ktorých jedna bola . Najdite prácu, ktorú sila pritom vykonala. V zadaní sú v sústave SI.

Odpoveď: .


D17. Malý krúžok hmotnosti sa pohybuje v horizontálnej rovine (bez trenia) po hladkom drôte ohnutom do tvaru oblúka kružnice s polomerom (obrázok, pohľad zhora). V bode 1 , kde rýchlosť krúžku bola , začala naň pôsobiť konštantná horizontálna sila s veľkosťou . Najdite rýchlosť v bode 2 .

Odpoveď: .


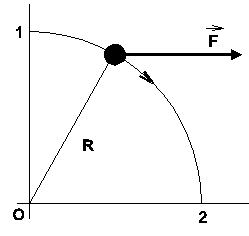
D18. Kinetická energia častice, pohybujúcej sa po kružnici s polomerom R , závisí od prejdenej dráhy s  ako , kde je konštanta. Najdite veľkosť sily, pôsobiacej na časticu, ako funkciu od s .

Odpoveď: .


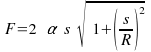D19. Teleso o hmotnosti m sme pomaly vytiahli na kopček (obrázok), pôsobiac silou , nasmerovanou v každom mieste v smere tangenty k trajektórii. Najdite prácu tejto sily, ak výška kopčeka je h , dĺžka jeho základne je l a koeficient trenia medzi telesom a podložkou je k .

Odpoveď: .


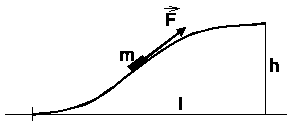
D20. Sústava pozostáva z dvoch za sebou spojených pružín s tuhosťami . Vypočítajte prácu, ktorú treba vynaložiť na predĺženie tejto sústavy o .

Odpoveď: .


D21. Hladká gumová šnúra o dĺžke l sa chová ako pružina s tuhosťou . Jedným koncom je zavesená v určitom bode O a na spodnom konci je vybavená zarážkou. Z bodu O pustíme krúžok o hmotnosti m , navlečený na gumu, ktorý môže po nej padať bez trenia. Zanedbajte hmotnosť šnúry a zarážky a vypočítajte maximálne predĺženie šnúry !

Odpoveď: .


D22. Sústava pozostáva z dvoch rovnakých kociek, každej s hmotnosťou m , medzi ktorými je stlačená pružina tuhosti k . Kocky sú zviazané niťou (obrázok), ktorú v určitý moment prestrihneme. Pri akých hodnotách počiatočného stlačenia pružiny spodná kocka podskočí po prestrihnutí nite ?

Odpoveď: > .


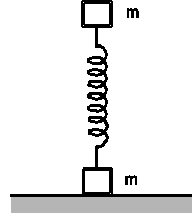
D23. Letiaci náboj z pušky o hmotnosti m uviazol v strede dreveného valca o hmotnosti M a zaveseného na lankách o dĺžke l (obrázok). Lanká sa od zvislého smeru odchýlili o uhol . Za predpokladu, že M >>m , vypočítajte :

a) rýchlosť náboja pred nárazom na valec,

b ) relatívnu časť kinetickej energie náboja,ktorá sa premenila na vnútornú energiu.

Odpoveď: a) , b) .


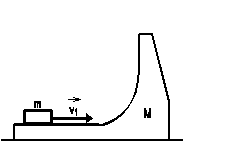
D24. Na hladkej horizontálnej rovine sa nachádza teleso o hmotnosti M , ktoré sa môže pohybovať po vodorovnej rovine bez trenia. Na ňom je položené iné teleso o hmotnosti m (obrázok). Tomuto druhému telesu sme udelili v horizontálnom smere rýchlosť . Do akej výšky H nad pôvodnú (začiatočnú) výšku vyletí toto teleso po oddelení sa od telesa M ? Trenie sa v celej úlohe neuvažuje.

Odpoveď: .


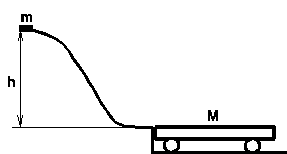
D25. Kváder o hmotnosti m spustíme zo šmykľavého kopčeka (bez trenia) o výške h , ktorý sa dole začne šmýkať po doske o hmotnosti M s trením (obrázok). Doska je uložená na ložiskách, aby sme trenie medzi ňou a podlahou mohli zanedbať. Po určitom čase sa doska pohybuje už spolu s kvádrom, ktorý sa vďaka treniu na nej zastavil. Vypočítajte prácu síl trenia pri takomto procese.

Odpoveď: .


D26. Najdite prírastok kinetickej energie sústavy dvoch guliek s hmotnosťami a rýchlosťami , ku ktorému prišlo po ich absolútne nepružnej zrážke (pri uvedenej zrážke sa obe telesá spoja do jedného s hmotnosťou ).

Odpoveď: .


D27. Na hladkej horizontálnej rovine ležia 3 rovnaké kotúče A, B, C (obrázok). Kotúču A sme udelili horizontálnu rýchlosť takým spôsobom, že súčastne pružne narazil do oboch kotúčov B a C . Vzdialenosť medzi stredmi kotúčov B a C do zrážky bola - krát väčšia ako je priemer kotúčov. Najdite rýchlosť kotúča A po náraze a tiež určte, pri akých hodnotách sa kotúč A odrazí spätne alebo zostane stáť alebo pôjde v pôvodnom smere.

Odpoveď: <> .


D28. K bodu s polohovým vektorom vzhľadom na začiatok vzťažnej sústavy je priložená sila , pričom a , b , A , B sú konštanty, sú vektory ortonormovanej bázy. Najdite moment a rameno sily F vzhľadom na momentový bod O !

Odpoveď: .


D29. Moment hybnosti častice vzhľadom na momentový bod O sa mení s časom podľa formuly , kde sú konštantné vektory, pričom . Najdite moment sily vzhľadom na O , pôsobiacej na časticu v momente, keď uhol medzi vektormi a L je .

Odpoveď: .


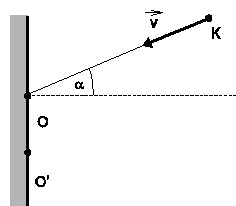
D30. Kotúč K  hmotnosti m sa šmýka po hladkej horizontálnej rovine rýchlosťou v a v bode (obrázok) sa pružne odrazí od hladkej pevnej steny. Uhol medzi smerom pohybu kotúča a normálou ku stene je . Najdite:

a) body, vzhľadom na ktoré zostane moment hybnosti kotúča v uvedenom procese konštantný,

b) veľkosť prírastku momentu hybnosti kotúča vzhľadom na bod , ktorý sa nachádza v rovine pohybu kotúča vo vzdialenosti s od bodu .

Odpoveď: a) Hľadané body všetky ležia na priamke kolmej na rovinu odrazu a idúcu bodom , b) .


D31. Vertikálny valec je upevnený na hladkej horizontálnej rovine. Na valec je tesne namotaná niť, ktorej voľný koniec je spojený s neveľkým kotúčom K  o hmotnosti (obrázok, pohľad zhora). Kotúču sme udelili horizontálnu rýchlosť smerom kolmo na napnutú niť. Vypočítajte moment hybnosti kotúča vzhľadom na vertikálnu os C tvoriacu os valca ak viete, že sila, pri ktorej sa niť roztrhne, je .

Odpoveď: .


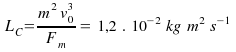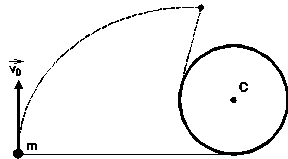
D32. Na hladkej horizontálnej rovine sa pohybuje malé teleso s hmotnosťou m , priviazané k pevnej niti, ktorej druhý koniec vťahujeme cez dierku O v rovine smerom nadol konštantnou rýchlosťou (obrázok). Vypočítajte silu napnutia nite v závislosti od vzdialenosti r telesa od dierky, ak pri bola uhlová rýchlosť nite rovná !

Odpoveď: .


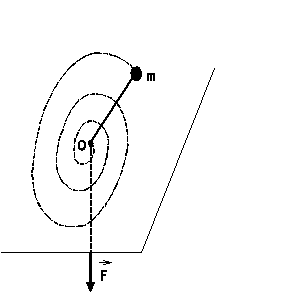
D33. Na vnútornej strane kužela, stojaceho vertikálne vrcholom dolu, kĺže malá guľôčka (obrázok) z toho dôvodu, že sme jej vo vertikálnej výške nad rovinou, v ktorej leží vrchol, udelili v horizontálnom smere rýchlosť . Na akú najväščiu výšku h sa guľôčka dostane pri svojom pohybe ? (Pomôcka: Výšku h vypočítajte z funkcie (h) .)

Odpoveď: .











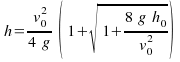Elektrostatika



ES 1. Vypočítajte, akou silou by na seba pôsobili dve malé medené guľky, každá s hmotnosťou , keď by boli vo vzdialenosti od seba a ak by sa absolútna hodnota sumárneho náboja všetkých elektrónov líšila o 1 % od sumárneho náboja všetkých jadier ! (Atómová hmotnosť medi je a at. číslo 29 .)

Odpoveď: !!


ES 2. Dve malé rovnaké guľôčky hmotnosti m sú nabité rovnakým elektrickým nábojom. V jednom bode sú zavesené na hodvábnych nitiach o dĺžkach l a vzdialené od seba x , pričom x << l . Najdite rýchlosť úniku náboja z guľôčok, , ak sme namerali, že rýchlosť približovania sa guľôčok sa mení podľa vzťahu , kde b  je konštanta.

Odpoveď: .


ES 3. Tenké vodivé kruhové vlákno s polomerom nesie rovnomerne rozložený náboj . Aký bude prírastok sily rozťahujúcej vlákno, ak do stredu vlákna umiestnime bodový náboj ?

Odpoveď: .


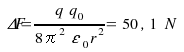ES 4. Sústava pozostáva z tenkého nabitého krúžku s polomerom R a veľmi dlhej rovnomerne nabitej nite, natiahnutej v osi krúžku tak, že jeden jej koniec začína práve v strede krúžku. Krúžok je rovnomerne nabitý nábojom q a náboj jednotkovej dĺžky nite je . Najdite silu vzájomného pôsobenia krúžku a nite.

Odpoveď: .


ES 5. Tenký nevodivý krúžok o polomere R je nabitý elektrickým nábojom s lineárnou hustotou ( je náboj, pripadajúci na jednotku dĺžky krúžku), kde je polárny uhol, odčítaný od Z - ovej osi, orientovanej jednotkovým vektorom k . Najdite intenzitu elektrického poľa E v strede krúžku.

Odpoveď: .


ES 6. Dve paralelné veľmi dlhé nite sú rovnomerne nabité s lineárnou hustotou náboja a sú vzdialené od seba . Najdite maximálnu hodnotu veľkosti elektrického poľa v rovine symetrie tejto sústavy, ležiacej medzi nimi.

Odpoveď: .


ES 7. Vypočítajte potenciál a veľkosť intenzity elektrického poľa v strede polosféry s polomerom r , ktorá je rovnomerne nabitá nábojom s plošnou hustotou .

Odpoveď: .


ES 8. Vypočítajte potenciál nasledujúcich elektrických polí ( i , j , k tvoria ortonormovanú bázu):

a)

b)

c) .

d) Homogénneho elektrického poľa .

Odpoveď: a) , b) , c) ,

d) , r – polohový vektor bodu v priestore.


ES 9 . Tenký guľový vodivý plášť o polomere R je nesený nevodivou tyčinkou a je nabitý na potenciál . Elektrón vystrelíme zo vzdialenosti r od stredu nabitej gule priamo na jej stred rýchlosťou . a) Aká má byť rýchlosť , aby elektrón dosiahol práve plášť gule, keď ? b) Upravte výsledok pre prípad, že r >> R . Aká má byť rýchloť v takomto prípade ? (Náboj elektrónu je , hmotnosť .)

Odpoveď : a) , b) .


ES 10. Dve planparalelné kovové dosky sú od seba vzdialené o d a sú spojené vodičom. Medzi nimi je natiahnutá blana z plastickej látky, ktorá je rovnomerne nabitá nábojom z plošnou hustotou . Najdite intenzity elektrického poľa blízko hornej a dolnej dosky ako funkcie vzdialenosti x blany od hornej dosky. (Rozmery dosák sú oveľa väčšie ako vzdialenosť dosák.)

Odpoveď: .


ES 11. Vypočítajte potenciál dosky o ploche S nabitej rovnomerne nábojom vzhľadom na paralelnú, rovnako veľkú dosku nabitú nábojom , keď ich vzdialenosť je d a sú vo vákuu. Okrajové efekty neuvažujte.

Odpoveď : .


ES 12. Majme tri paralelné kovové dosky A, B, C, z ktorých A a B sa na začiatku dotýkajú a medzera medzi doskou B a C je vtedy d . Potenciálny rozdiel medzi krajnými doskami A a C je stále udržiavaný batériou o elektromotorickom napätí . Pomocou izolovanej rúčky posunieme paralelne strednú dosku B tak, že medzera medzi A a  B bude široká x . Pri zanedbaní okrajových efektov najdite intenzitu elektrických polí v medzerách medzi AB a BC ako funkciu vzdialenosti x . Zvoľte jednotkový vektor i v smere od dosky A k doske B .

Odpoveď: .


ES 13. Dve nekonečné planparalelné kovové dosky sú vo vákuu vzájomne nehybné. Prvá doska (povedzme vľavo) je nabitá tak, že celkový náboj pripadajúci na jej jednotkovú plochu je konštantný a rovný , zatiaľ čo u druhej dosky (teda vpravo) je to podobne (rozmer týchto veličín je teda ).

a) Vypočítajte intenzitu elektrického poľa vľavo od prvej dosky, - medzi doskami a - vpravo od druhej dosky. Výsledky napíšte vo vektorovej forme, pričom zvoľte jednotkový vektor i  v smere kolmo od prvej dosky ku druhej doske. Vypočítajte tiež

b) plošné hustoty nábojov na (štyroch) povrchoch dosák, zľava postupne označených ako .

Odpoveď: a) ,

b) .


ES 14. Dve vodivé dosky rovinného kondenzátora sú navzájom vzdialené o d . Medzi tieto dosky vložíme ďalšiu nenabitú kovovú dosku hrúdky tak, že je rovnobežná s predošlými doskami a jej vzdialenosť od bližšej dosky kondenzátora je . Aký je potenciál vloženej dosky, keď potenciál bližšej dosky udržiavame na hodnote a druhej dosky na hodnote ? Počítajte najprv všeobecne, a potom vyčíslite pre konkrétne hodnoty : Okrajové efekty neuvažujte .

Odpoveď : . Tu je vzdialenosť vloženej dosky od druhej dosky s potenciálom .


ES 15. Najdite potenciál na okraji disku s polomerom R , ktorý je rovnomerne nabitý nábojom s plošnou hustotou .

Odpoveď: .


ES 16. Do dutej vodivej gule s vnútorným polomerom a vonkajším polomerom sme umiestnili bodový náboj q vo vzdialenosti r < od ich spoločného stredu O . Najdite potenciál v bode O !

Odpoveď: .


ES 17. Sústava sa skladá z dvoch koncentrických vodivých sfér s polomermi , <. Na vnútornej sfére je náboj . Aký náboj treba priviesť na vonkajšiu sféru, aby bol potenciál vnútornej sféry ? Vzťažný bod je zvolený v nekonečnu, kde je potenciál nulový. Najdite aj potenciál ako funkciu r , kde r je vzdialenosť od stredov sfér.

Odpoveď: .


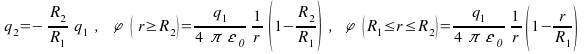ES 18. Priestor je zaplnený nábojom s objemovou hustotou , kde a sú kladné konštanty a r je vzdialenosť od stredu sústavy nábojov. Najdite veľkosť intenzity elektrického poľa ako funkciu r . Ako sa chová táto intenzita pri malých a veľkých r, t.j. pri << 1 a >> 1 ?

Odpoveď : , E(<< 1) , E(>> 1) 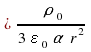, čo je intenzita ako pre bodový náboj.


ES 19. Guľovo symetrické, ale nehomogénne rozloženie elektrického náboja vytvára elektrické pole o veľkosti , smerujúce radiálne von zo stredu gule, pričom r je radiálna vzdialenosť od stredu. Aká je objemová hustota náboja , ktorá vytvára takéto pole ?

Odpoveď : .


ES 20. Veľmi tenký disk je rovnomerne nabitý nábojom s plošnou hustotou > 0 . Najdite intenzitu E elektrického poľa na osi disku v mieste, z ktorého vidíme disk pod priestorovým uhlom .

Odpoveď : .


ES 21. Intenzita elektrického poľa závisí iba od súradníc x a y podľa vzťahu , kde a je konštanta a sú jednotkové vektory v smere osí X , Y. Najdite tok vektora E cez sféru o polomere R so stredom v začiatku vzťažnej sústavy.

Odpoveď : .


ES 22. Najdite silu F, ktorou pôsobí elektrický dipól s momentom p na bodový náboj q , ak je medzi nimi vzdialenosť r a p smeruje na bodový náboj.

Odpoveď : .


ES 23. Najdite silu, ktorou pôsobí dipól na dipól , keď oba dipóly smerujú podĺž ich spájajúcej priamky určenej jednotkovým vektorom k a ich vzdialenosť je r . Kedy sa dipóly budú priťahovať a kedy odpudzovať ?

Odpoveď : 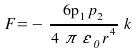, takže dipóly sa budú priťahovať, ak ↑↑ a odpudzovať, ak ↑↓ .


ES 24. Zistite, či sa môže nabitá častica pohybovať po kružnici v elektrickom poli nehybného bodového dipólu konštantnou rýchlosťou. Kvôli označeniu vložte dipól do začiatku vzťažnej sústavy a nech má smer vektora k Z-ovej osi.

Odpoveď : Je to možné v prípade, že polohový vektor častice je stále odkolonený od Z-ovej osi o polárny uhol , pre ktorý platí , kde horné znamienko platí pre záporne nabitú časticu, dolné pre kladne nabitú časticu.


ES 25. Sféra o polomere r je nabitá nábojom s plošnou hustotou , kde je konštantný vektor a r je polohový vektor bodu sféry vzhľadom na jej stred. Najdite vektor intenzity elektrického poľa v strede sféry.

Odpoveď: .


ES 26. Vypočítajte intenzitu elektrického poľa E v oblasti prieniku dvoch gúľ, rovnomerne nabitých spojitými elektrickými nábojmi opačného znamienka s hustotou (> 0 ), ak je stred kladne nabitej gule posunutý o vektor l vzhľadom na stred záporne nabitej gule.


Odpoveď : . Komentár: Výsledok je platný bez ohľadu nato, aké sú polomery oboch gúľ a aká je vzdialenosť ich stredov (pokiaľ je ich prienik nenulová množina). Teda aj v prípade, keď sa jedna guľa celá nachádza v druhej guli. Inými slovami aj vtedy, ak je v homogénne nabitej guli (napr. pri > 0 ) vytvorená nenabitá guľová dutina, posunutá v uvažovanom prípade o vektor vzhľadom na (kladne) nabitú guľu. Výsledok môžeme prepísať na zaujímavý a dôležitý tvar, ak posunutie l nahradíme veľmi malým posunutím (rádove zlomku polomeru atómov látky). Vtedy možno napísať pre vektor polarizácie látky vzťah (podľa definície). Z toho vyplýva, že intenzita elektrického poľa vo vnútri homogénne sporarizovanej dielektrickej gule je .


ES 27. Vypočítajte intenzitu elektrického poľa v guľovej dutine vytvorenej v nekonečne rozľahlom homogénne spolarizovanom dielektriku. (Návod: Využite výsledok predchádzajúcej úlohy a uplatnite princíp superpozície.)

Odpoveď : , kde E je intenzita poľa v dielektriku a je relatívna permitivita uvažovaného dielektrika.


ES 28. Doštičku z ebonitu hrúbky d a plochy S sme vložili do homogénneho elektrického poľa o intenzite tak, že siločiary poľa sú na ňu kolmé. Vypočítajte: a) plošnú hustotu polarizačných (viazaných) nábojov na povrchu doštičky, b) energiu elektrického poľa obsiahnutú v dielektriku. (Číselné údaje: . )

Odpoveď : .


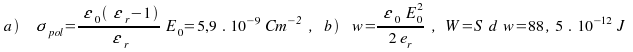ES 29. Medzi dve paralelné nenabité vodivé dosky, ktoré sú prepojené vodičom a vzdialenosť ktorých je d , sme paralelne vsunuli spolarizovanú elektretovú dosku hrúbky h . (Elektret je materiál, ktorý môže mať trvalý nenulový vektor polarizácie, aj keď nie je polarizovaný vonkajším elektrickým poľom, čo je náš prípad.) Vektor polarizácie dosky P je kolmý na plochu dosky. Pri zanedbaní závislosti polarizácie P od elektrického poľa, vypočítajte intenzitu a indukciu elektrického poľa vo vnútri a  zvonku elektretovej dosky. Aby sme mohli výsledok uviesť vo vektorovom tvare, zvolíme si jednotkový vektor k v smere P .

Odpoveď : .


ES 30. Medená guľa s polomerom R je polovicou svojho objemu ponorená v oleji s permitivitou a druhou polovicou vo vode s permitivitou a je nabitá nábojom Q . Aký je potenciál a intenzita elektrického poľa na jej povrchu ?

Odpoveď : .


ES 31. Guľový kondenzátor pozostáva z dvoch koncentrických gúľ s polomermi , < , medzi ktorými je dielektrikum o permitivite . a) Vypočítajte kapacitu tohoto kondenzátora. b) Určte, aký má byť pomer , ak má byť pri danom napätí U na kondenzátore intenzita minimálna.

Odpoveď : a) ,   b) .


ES 32. Majme vzduchový doskový kondenzátor, ktorý nabijeme na rozdiel potenciálov a zdroj odpojíme. Potom vsunieme do polovice dielektrickú doštičku s relatívnou permitivitou . Určte: a) akou silou sa priťahujú dosky kondenzátora , b) polarizáciu dielektrika. Výsledky vyčíslite nakoniec pre nasledovné údaje: čo je aj hrúbka doštičky, plocha dosák . (Návod: Silu, ktorou sa priťahujú dosky určte zo vzťahu , kde index znamená, že treba hľadať diferenciál energie kondenzátora pri konštantnom náboji na ňom. Posunutie je fiktívne posunutie dosák, ktorým by sme pri ťahaní silou F zvýšili energiu kondenzátora.)

Odpoveď : a) 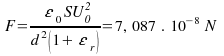, b) .


ES . Bodový náboj Q sa nachádza v strede konečne hrubej guľovej vrstvy z nehomogénneho a izotrópneho dielektrika, relatívna permitivita ktorého závisí od vzdialenosti r od stredu symetrie sústavy ako , kde je konštanta. Najdite objemovú hustotu viazaných nábojov vo vnútri vrstvy ako funkciu r .

Odpoveď : .


ES 34. Máme k dispozícii tri kondenzátory s dovolenými napätiami . Pri akom zapojení týchto kondenzátorov možno získať najväčšie prípustné napätie ? Čomu sa rovná toto napätie a aká je pritom kapacita batérie ?

Odpoveď : Zapojenie do série, .


ES 35. Kondenzátory sú zapojené podľa schémy na obrázku na zdroj o elektromotorickom napätí . V zapojení sú dva spínače . Vypočítajte elektrické náboje na každom kondenzátore a) najprv pre prípad, že je zopnutý iba spínač , b) zopnuté sú oba spínače. Kapacity kondenzátorov sú postupne .

Odpoveď : a) ,

 
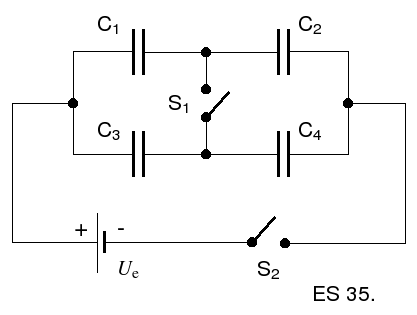
                   b) .



ES 36. Najdite rozdiel potenciálov medzi bodmi A a B schémy na obrázku.

O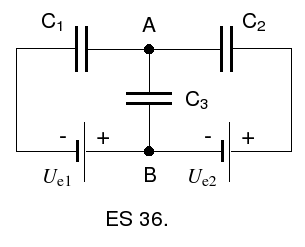
dpoveď : .



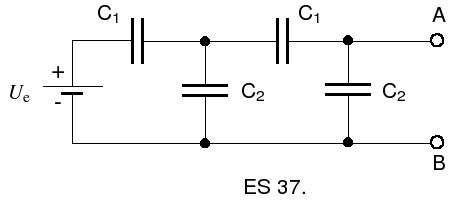
ES 37. V schéme na obrázku najdite rozdiel potenciálov medzi bodmi A a B , ak elektromotoricé napätie a pomer kapacít kondenzátorov .

Odpoveď : .





E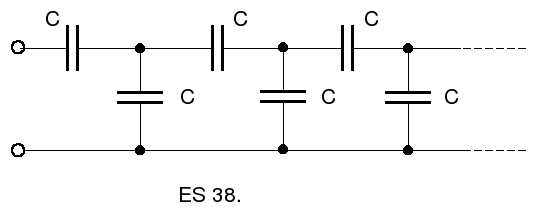
S 38. Vypočítajte kapacitu nekonečnej kaskády kondenzátorov na obrázku, keď kapacita všetkých použitých kondenzátorov je C .

Odpoveď : .


ES 39. Rovinný vzduchový kondenzátor o kapacite je nabitý na rozdiel potenciálov . Po odopnutí kondenzátora od zdroja sme 5 – krát pomaly zväčšili medzeru medzi doskami. Najdite : a) rozdiel potenciálov na doskách po roztiahnutí dosiek od seba, b) prácu externých síl pri rozťahovaní dosiek.

Odpoveď : a) ,   b) .


ES 40. Otočný kondenzátor má kapacitu . Pri maximálnej kapacite ho nabijeme na napätie U . Potom ho odpojíme od zdroja napätia a otočíme ho do polohy, v ktorej má kapacitu . Akú prácu pritom vykonáme, ak neuvažujeme prácu pri trení ?

Odpoveď : .


ES 41. Dva kondenzátory o kapacitách a nabijeme tak, že nesú náboje a . Ukážte, že okrem špeciálnych prípadov, elektrická energia sa v kondenzátoroch zmenší, ak spojíme spolu ich kladné a záporné dosky (zapojíme ich teda paralelne). Najdite podmienky, pri ktorých spojenie kondenzátorov nemá za následok stratu v nich obsiahnutej energie.

Odpoveď : Rozdiel v energiách sa vyžiari (a prípadne premení na teplo v spojovacích vodičoch). K strate energie obsiahnutej v kondenzátoroch nepríde, ak je splnená podmienka .


ES 42. Vypočítajte, aký je rozdiel medzi energiou elektrického dipólu, ktorý vytvoríme postupným prinesením jeho nábojov a z nekonečna do miesta vonkajšieho elektrického poľa o intenzite E a energiou, keď do tohoto miesta vonkajšieho poľa prinesieme z nekonečna už hotový dipól !

Odpoveď : Rozdiel energií je , kde je vzdialenosť medzi nábojmi a . Je to práve interakčná energia medzi nábojmi dipólu.


ES 43. Tri rovnaké guľôčky sú uložené vo vrcholoch rovnostranného trojuholníka so stranou a a sú navzájom pospájané niťou. Všetky sú nabité rovnakým nábojom q a majú aj rovnakú hmotnosť m . V istom okamihu jednu z nití prepálime. Najdite maximálnu rýchlosť strednej guľôčky. Tiažové sily neuvažujte. (Návod: Použite zákon zachovania hybnosti a energie sústavy.)

Odpoveď: .