13.3.3 Matematické vyjadrenie de Broglieho vĺn a jeho fyzikálny význam

13.3.3.1 Vlnová funkcia a jej význam

V dobe vzniku myšlienky „hmota má ako časticové tak i  vlnové vlastnosti“, nebola De Broglieho teória podporená silným experimentom, ako tomu bolo napríklad pri fotoefekte alebo žiarení zahriatych telies. De Broglie pri vyslovení svojej hypotézy neuviedol podrobnejší popis vlny hmoty, len jej priradil vlnovú dĺžku, určenú rovnicou 13.3.2.1.

Je vhodné sa zamyslieť nad otázkou: Akého druhu sú vlnové javy v prípade de Broglieho vĺn?

Vo svetelnej vlne sa mení v priestore a v čase elektromagnetické pole. Vo zvukovej vlne je to tlak. Aká to bude veličina, ktorej zmeny vytvárajú de Broglieho vlnu?

Zaveďme pojem - vlnová funkcia Y (grécke písmeno Y čítaj psí) ako veličinu, ktorá charakterizuje de Broglieho vlny. Hodnota tejto vlnovej funkcie, prináležiacej pohybujúcej sa častici (telesu) v danom bode priestoru so súradnicami [x, z, y] v čase t, súvisí s pravdepodobnosťou výskytu častice v danom bode a čase. Nakoľko amplitúda každej vlny môže nadobúdať ako kladnú tak i zápornú hodnotu, Y ako pravdepodobnosť, nemôže byť záporná. Z tohto dôvodu samotná vlnová funkciaY nemá fyzikálny význam. Y sama o sebe nemôže byť pozorovateľná veličina.

Poznámka: Pravdepodobnosť P, že častica sa v danom okamihu bude nachádzať niekde, znamená že môže nadobúdať hodnoty z intervalu < 0, 1> . P = 0 znamená, že častica sa v danom bode nenachádza. P = 1 znamená 100 % istotu, že častica sa nachádza v danom bode.

Fyzikálny význam však má druhá mocnina absolútnej hodnoty vlnovej funkcie ½y½², ktorá sa nazýva hustotou pravdepodobnosti . Pravdepodobnosť experimentálneho zistenia mikročastice, popísanej vlnovou funkciou Y v bode A so súradnicami [x, z, y] v čase t v jednotkovom objeme v okolí bodu A, je úmerná hodnote½y½². Pravdepodobnostnú interpretáciu nájdenia častice prvýkrát zaviedol Max Born v roku 1926.

Pri takomto pravdepodobnostnom prístupe si treba uvedomiť, že aj keď vlnová funkcia, ktorá popisuje časticu, sa bude rozprestierať v priestore, neznamená to, že častica je tiež rozprestretá v priestore. V prípade detekcie elektrónov na detektore alebo fotografickej platni pri difrakcii elektrónov na dvoch štrbinách, buď nájdeme v danom okamihu celý elektrón, alebo v tomto čase žiaden elektrón nezaregistrujeme.

Vlnová funkcia, popisujúca stav častice, môže byť vo všeobecnosti komplexnou funkciou, s nenulovou reálnou i imaginárnou časťou, t.j. možno ju zapísať v tvare

y = A + Bi,

kde A a B sú reálne funkcie. V tomto prípade bude hustota pravdepodobnosti výskytu určená súčinom yy^*, kde

y^* = A - Bi,

½ y½² = yy^* = A² +B². (13.3.3.1)

Z poslednej rovnice vyplýva, že hustota pravdepodobnosti výskytu častice v jednotkovom objeme v okolí bodu A s polohovým vektorom r v čase t je vždy nezáporná reálna veličina.

Poznámka: Komplexne združenú funkciu k akejkoľvek funkcii nájdeme, ak uskutočníme zámenu i Þ -i, všade kde sa vo funkcii vyskytuje. Majme na pamäti, že platí i² = - 1

––––––––––––––––––––––––––––––––––––––––––––––––

Príklad 13.3.3.1 Nájdite komplexne združenú funkciu k vlnovej funkcii častice opísanej na úsečke určenej intervalom (0,L) rovnicou y(x, t) = A exp (-i2pEt/h) sin p x/L .

Riešenie: Určíme komplexne združenú funkciu k funkcii y zámenou i Þ -i,

y^*(x, t) = A exp [-(-i)2pEt/h] sin p x/L = A exp (i2pEt/h) sin p x/L .

________________________________________________

Ak dV je objemový element v okolí bodu A , potom pravdepodobnosť P nájsť časticu v čase t v objeme V je

(13.3.3.2)

V prípade, ak nám stačí sa obmedziť na jednorozmerný prípad, (napríklad pohyb častice v smere osi x), objemový element dV nahradíme veľkosťou intervalu dx a pravdepodobnosť P_x nájsť časticu v intervale dx v okolí bodu A v čase t je

(13.3.3.3)

Skutočnosť, že častica sa v objeme V nachádza, vyjadruje normovacia podmienka

(13.3.3.4)

respektíve pre časticu nachádzajúcu sa niekde na osi x

(13.3.3.5)

Vlnové funkcie, ktoré spĺňajú normovaciu podmienku (13.3.3.4), respektíve (13.3.3.5), nazývame normované vlnové funkcie.

Na základe pravdepodobnostného prístupu možno experiment na obr. 13.3.1.3 interpretovať nasledovne: červenú krivku ako pravdepodobnosť P₁ =½Y₁ ½², modrú krivku ako pravdepodobnosť výskytu P₂ =½Y₂ ½² a zelenú ako pravdepodobnosť výskytu P₁+ P₂ =½Y₁½² +½Y₂½^{2 .} Pozorovaná skutočnosť P (čierna krivka) však naznačuje, že hoci nevieme určiť, ktorým otvorom elektrón prešiel, vlny pravdepodobnosti interferovali a vytvorili obraz, ktorý vyjadruje pravdepodobnosť výskytu P =½k₁Y₁ +k₂Y₂½², kde k₁ a k₂ sú koeficienty, charakterizujúce priepustnosť jednotlivých štrbín. Keďže výsledné vlnenie je superpozíciou jednotlivých vlnení, možno si uvedomiť, že princíp superpozície platí i  pre de Broglieho vlny.

––––––––––––––––––––––––––––

Príklad 13.3.3.2 Určite konštantu A, tak aby funkcia Y(x)= A sin (npx/L) , kde n, A a L sú konštanty , bola normovanou vlnovou funkciou na intervale <0, L >.(Vlnová funkcia mimo tento interval je nulová.)

Riešenie: Aby vlnová funkcia bola normovanou vlnovou funkciou na na intervale <0, L >. musí spĺňať podmienku

Nakoľko vlnová funkcia je reálna funkcia, komplexne združená funkcia je taká istá, takže platí

.

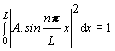Vypočítajme ľavú stranu rovnice:

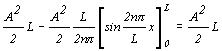
Porovnaním s ľavou stranou dostávame pre konštantu A hodnotu

.

––––––––––––––––––––––––––––

Ako nájdeme vlnové funkcie v konkrétnych situáciách? Na túto otázku nájdeme odpoveď v  časti 13.4 , pojednávajúcej o základnej rovnici kvantovej fyziky, Schrödingerovej rovnici.

Kontrolné otázky:

1. Vyslovte základnú myšlienku Maxa Borna spojenú s významom vlnovej funkcie popisujúcej mikročasticu?

2. Má fyzikálny význam samotná vlnová funkcia y (x,z,y,)?

3. Ktorá veličina vyjadruje hustotu pravdepodobnosti výskytu častice v jednotkovom objeme v okolí bodu A s polohovým vektorom r v čase t?

4. Vysvetlite z pravdepodobnostného hľadiska experiment na obr. 13.3.1.3.

5. Vyjadrite skutočnosť, že častica sa nachádza na osi x a pohybuje sa v intervale < a, b>.

6. Vysvetlite, čo sú normované vlnové funkcie a zapíšte normovaciu podmienku.

7. Platí princíp superpozície pre de Broglieho vlny?